引言
好久没有冒泡啦,宅着抗疫,得空把一些小思考总结一下,也算做点贡献。
一些学者已经开始从抗疫角度反思城市规划,很受启发。但主要集中反思城市规模、密度这些方面。甚至又有经济学家跳出来,一顿操作猛如虎,最后还是呼吁放开大城市人口、取消户籍制度、集体土地退出等等。这些讨论总感觉还差那么点儿意思。
遵循Elon Musk的第一原则,我们先思考抗疫的本质是什么?是如何与病毒在人群中的传播做对抗。如果病毒不能人传人、或者传播效率极低,那么就不需要全民抗疫,那么就与城市规模与密度没有关系。
而新冠肺炎可以人传人,且传播效率还不小。那么似乎城市人口规模越大、密度越高,病毒传播速度就越快,抗疫难度就越大。是这样吗?
随机网络
下面我们把城市抽象成一个“网络”来做实验。
所谓网络(Network/Graph),就是由节点(Node)和连接(Link/Edge)组成的抽象系统。病毒在人群中的传播,本质上是病毒在相互连接(存在接触)的节点(人)之间的传播。而不是像炸鱼一样,把鞭炮扔进河里,嘭的炸晕一群鱼。
我们首先来测试一个随机网络,即著名的Erdős-Rényi graph,又叫Gnp网络。所谓随机,是指给定一个节点数量n,它假设任意两点之间的连接以独立的概率p随机生成。Gnp随机网络是很重要的基准 (benchmark)。
我们假设有三个“城市”,分别有100,200,500个节点。分别控制每个城市的连接概率,使每个城市 节点平均连接数量 都等于6。也就是说,我们假设每个人交往精力有限,日常接触的朋友数量平均只有6个。通常我们称之为,度(的平均值)为6。

图:随机一个100节点、度为6的 Gnp网络
下面模拟病毒在其中的传播,我们随机一个网络,并且让病毒随机感染其中的一个节点,之后每次迭代(epoch) 使其以0.2的概率传染,然后考察传染的期望速度(感染的比例)。
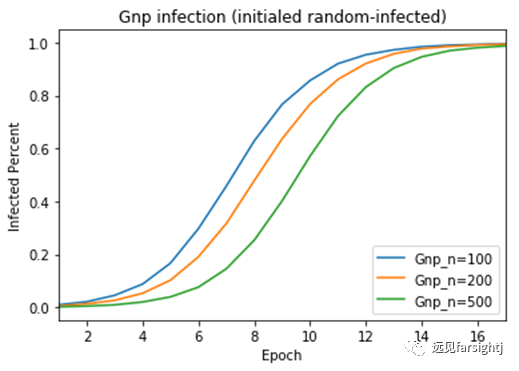
图:Gnp的病毒传播速度
结果却发现,越小的城市传播越快,越大的城市却传播越慢!
更接近现实的无标度网络
哪里有问题呢?第一,城市越大,网络的度——亦或节点的平均连接数量——显然不会保持不变,而是会越来越多才对。城市的魅力和某些集聚经济就在于此。
第二,一群人(比如一个年级)的社交网络可能像一个随机网络,确切的来说,它的度分布(每个节点拥有的连接数量的分布)偏向于正态分布。但是空间上的交往活动并非如此,更多的呈现幂分布。
比如下图是上海主要生活中心的活动密度-位序分布,可见极少数量的地方可能会有非常密集的接触可能,而大多数地方的活动更不密集。

图:上海主要生活中心的密度-位序分布
为了模拟病毒在这种幂分布网络中的传播,我们引入大名鼎鼎的Barabási–Albert preferential attachment model,也叫无标度网络 scale-free network,这里简称 Gba 网络。所谓preferential attachment 指的是一种马太效应,即新的节点与既有节点建立连接时,会有一种倾向于 度更高的节点(拥有最多连接的节点)的偏好。基于这种机制我们就能获得幂分布的网络。
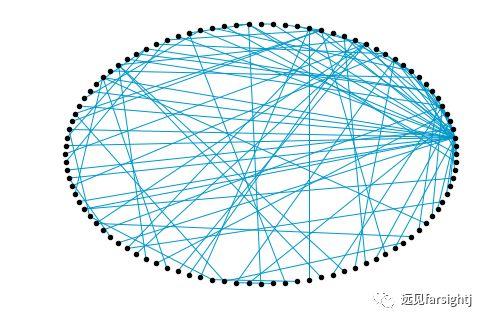
图:随机一个100节点的 Gba网络。可以看到少数节点有着大量连接,而大量节点只有1条连接。
我们同样假设有三个“城市”,分别有100,200,500个节点。同时我们假设三个城市里,每个新的节点分别与3、6、15个节点交往。也就是说,我们假设朋友数量与城市规模同比例增长。
然后模拟病毒在其中的传播。我们同样随机选择一个节点作为初始感染,当然也可以指定某个节点首先感染(比如度最高的节点),不影响对比结论。
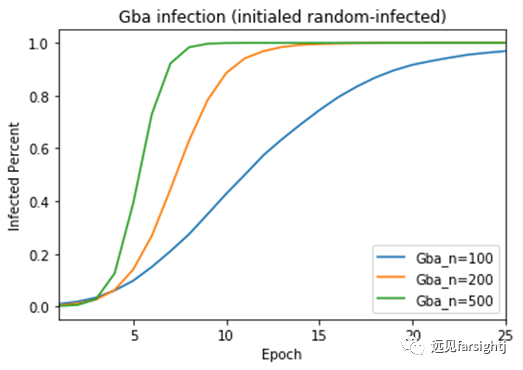
图:Gba的病毒传播速度
可见,大城市的风险十分突出。从1个人感染到100%感染,500的城市只需要100城市约1/5的时间!
显然,大城市的风险并不直接来自节点规模,而是来自网络的结构——更高的度 和 幂律分布的度,也就是 人均更多的交往数量 和 少数交往活动高度集聚的区位。
理想的抗疫网络
但以上结果模拟的是,病毒在正常运行的Gba城市中的传播。如果我们能够采取一定的抗疫措施,使得紧急状态下的城市能够维持运行并且有效降低病毒传播,那么显然,我们不仅不需要恐惧大城市,而且能够更好的思考应对策略。
实际上,如果我们仔细观察当前的严格抗疫状态,会发现它基本上符合一种树形的网络结构。我们呼吁每个人都宅在家里,并且仅开展必要的生活出行。
必要生活出行大致可以理解为获得基本公共服务的出行,包括:1. 基本的购物、放风等需求,这些活动可能在小区内就能解决;2. 基本的文教体卫需求,这些可能需要走出小区,前往街道、镇一级的公共设施解决;3. 小区服务者的批发等活动、外卖员的代购活动、快递员的收发活动、以及居民的特殊消费和公共服务可能需要前往更大的中心,当然频率更低 ……
这是一个完全树形的网络。它有点像中心地理论的图示,即每个人都严格的按照需求等级前往最近的对应中心活动。不同的是,最低层级不可以跳跃着直接联系到更高等级节点。整个系统如同一个分销网络,而这几乎就是理想的抗疫状态。
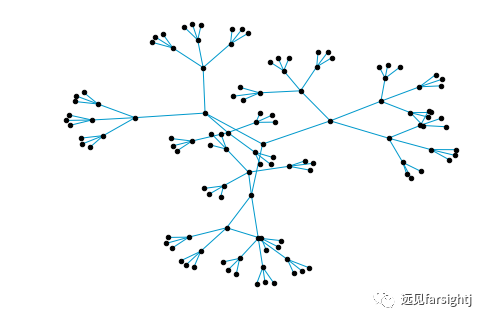
图:随机一个四层,每层向下新增三个节点的树(Balanced tree)
下面我们比较 随机网络Gnp,无标度网络Gba,树形网络Gtr 的传染效率。公平起见,三个城市的节点数量均设为1000,网络的度都控制为2(节点平均连接数量均为2),也就是说,总连接数量均控制在约1000。
我们随机许多许多次,每次按上述配置随机三个不同结构的城市,然后随机选择单个节点作为初始感染,最后以0.2的传染率考察整个系统的传染速度。结果如下:
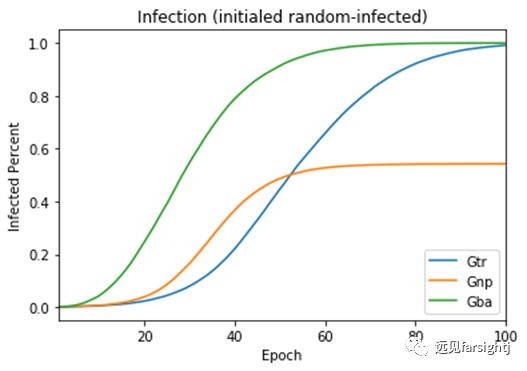
图:三种网络结构的病毒传播速度
我们可以看到,达到一半的传染比例、或者达到最高传染速度,树形网络Gtr的花费时间 比 无标度网络Gba 长了接近一倍!树形网络可以极大的降低传染速度。但因为网络是全连接的,两者最终都会逐渐把最远的节点全部传染。
而随机网络Gnp 虽然传染速度与 树形网络Gtr 差不多,但最终仅传染了约50%的人群。为什么呢?因为剩下的50%节点根本无法与外界连接! 也就是说,他们虽然不会被传染,但是会被饿死……
至此,我们获得了本文最重要的结论:
网络结构——亦或城市结构在抗疫中扮演着至关重要的作用。对于一个超大城市,它能够在正常运行时,在自由市场机制下形成类似 无标度网络 的结构,从而获得超高的集聚效益。但同时,它也应当建立完善一种树形网络,从而在紧急状态时既能保证所有节点的存活,又能极大的降低疾病传播速度。
矮胖树与高瘦树
那么是不是所有的树形结构都是好的呢?
我们进一步模拟三种树,他们都有1000个节点,分别以每次向下复制3、10、1000个节点的速度生成,即k=3,10,1000。换算之后,三种树的“高度”分别有7、4、2层,依次从最高最瘦 到 最矮最胖。
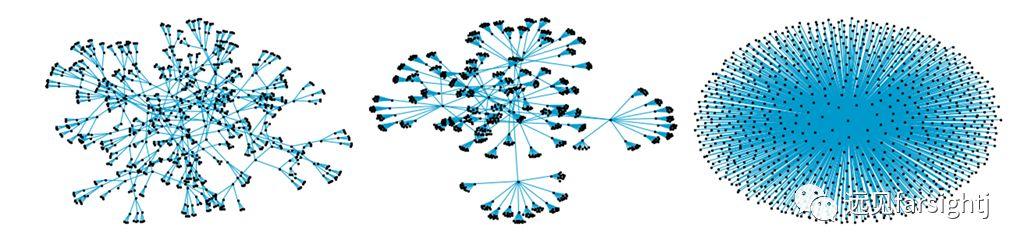
图:三种树
将三种树按生成时节点增长速率k分别命名为Gtree_3, Gtree_10, Gtree_1000。同样的随机模拟病毒在其中的传播速度:
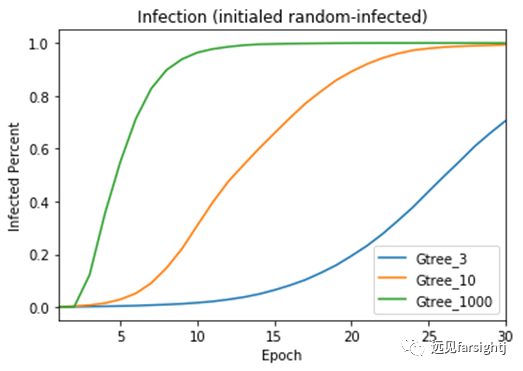
图:三种树的病毒传播速度
显然,越是高瘦树,传播效率越低。比如中心地理论 在市场原则下构造的树,其生长速度k为3;交通原则下生长速度k为4。而对于上海,通常认为的市级生活中心约有10个,地区级约有50个,街道单元约230个,居委单元约5400个。真实的k值略大于理论值。
但这仅仅是商品和生活服务供销的k值。如果我们考察中小学的网络结构,一个中小学约有上千的下层节点,基本上就是上述Gtree_1000的结构。它的病毒传染速度至少是 Gtree_3 的约5~6倍!实际上,被推到极端的Gtree_1000已经非常像无标度网络,它的传染速度甚至比无标度网络还要快。
结论与讨论
结论
-
正常情况下,越大的城市,病毒传播效率越高。但同时,越大的城市,其集聚效益也越高,意味可能更高的经济效率。
-
大城市的风险并非直接来自节点规模,而是来自网络结构——更高的度 和 幂律分布的度,也就是 人均更多的交往数量 和 少数交往活动高度集聚的区位。
-
为了应对紧急状态,越大的城市越应当建立完善一种树形网络。这种树形网络既要在正常时契合自由市场的某些规律,同时也要在紧急管制时既能为居民提供基本生活服务、保证所有节点的存活,又能极大的降低疾病传播速度。
-
这种树形网络不应是矮胖型,理论上看,k=3~5有一定的可行性。
-
对于某些设施,如果与之相关的树形网络结构是高瘦型,可考虑逐步放开与之相关的活动管控。而如果是矮胖型,例如学校系统,应考虑延迟放开管控。
讨论
首先,类似“15分钟生活圈”的规划政策与树形网络结构并不完全一致。如果政策目标仅仅是实现文教体卫商等基本公共服务的15分钟覆盖,这些每一类设施可能与小区之间形成树形结构,但总体上叠加后相互之间犬牙交错。即使在紧急管制状态下,仍会呈现树形+随机的结构。这种结构的病毒传播速度一定比树形结构更快,需要警惕。我以为,更应强调与城市中心体系相融合的生活圈政策。
其次,世界上不存在能抗疫的完美结构,哪怕是随机网络,我们每个人的参与和努力也会让它更好一些。针对传染病如此,谣言如此,知识与创新的传播更是如此。
最后,本文仅仅是抽象模拟,忽略了许多现实细节,例如,越是高瘦的树形网络,整体联系效率也就越低(diameter越高)。但正是抽象模拟能让我们直接思考问题本质,不是吗?
你还有什么想模拟的可以留言哦。
参考
A. L. Barabási and R. Albert “Emergence of scaling in random networks”, Science 286, pp 509-512, 1999.
P. Erdős and A. Rényi, On Random Graphs, Publ. Math. 6, 290 (1959).
Jackson, Matthew O. The Human Network: How Your Social Position Determines Your Power, Beliefs, and Behaviors. Pantheon, 2019.
原文始发于微信公众号(远见farsightj):网络、抗疫与城市规划
 健康城市:应对新冠疫情专栏
健康城市:应对新冠疫情专栏