上界映射与随机可视域——对比视线图分析系统的解决方案丨城市数据派

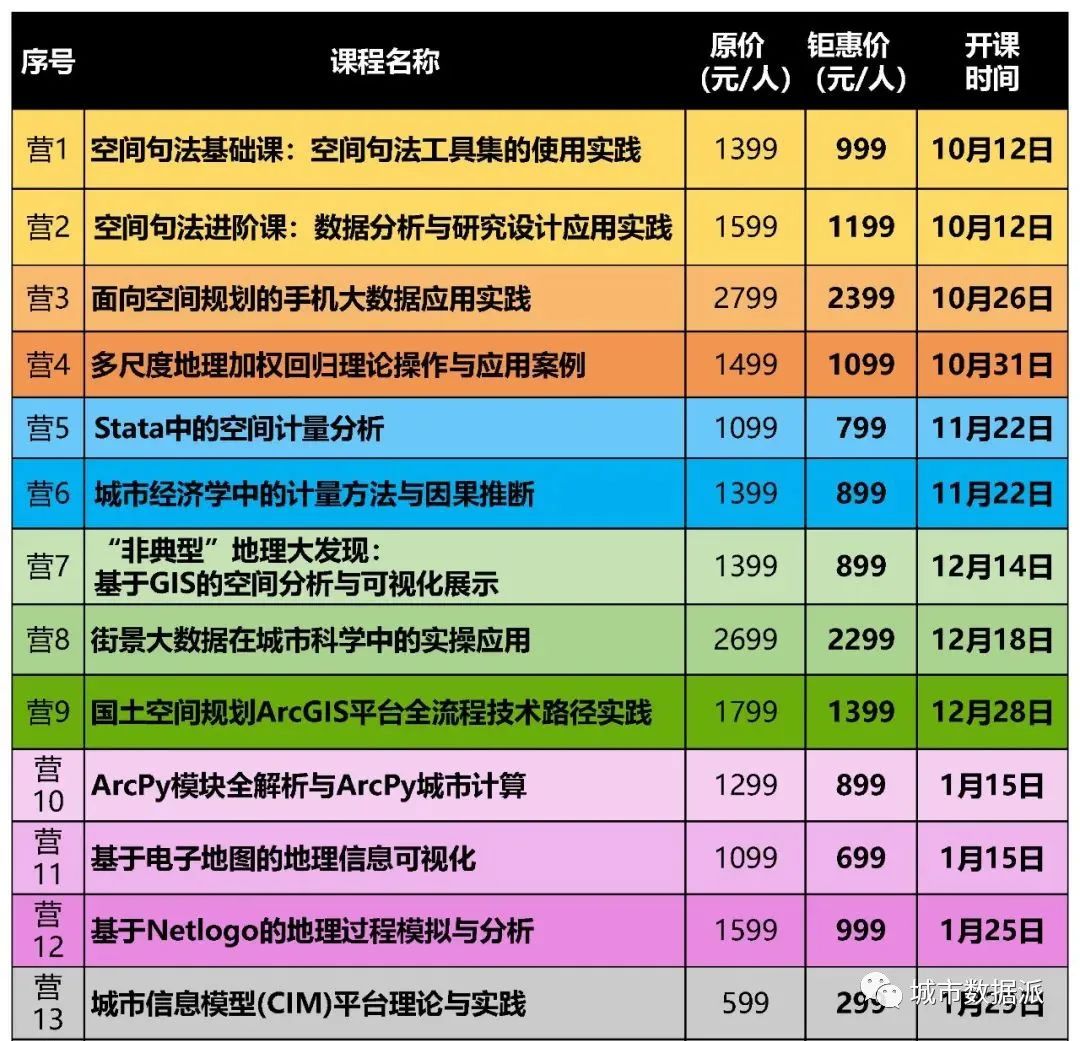
年终数据技能大冲刺开车啦！

同时报名还可享更多优惠：

任选2套同报，钜惠价再减200元！

任选3套同报，钜惠价再减360元！

任选4套同报，钜惠价再减520元！

任选5套同报，钜惠价再减650元！

（多套同报优惠到1月30日截止，

以上优惠不包括营13）

1 研究背景

视线图分析（visibility graph analysis, VGA） [1]是空间句法社区普遍用来评估城市和建筑设计的方法。为了比较不同的空间布局，建筑师和研究人员依赖基于 D 值标准化的整合度指标。本文指出，这种形式的标准化最初是为了凸空间分析和轴线分析而开发的。它们与典型 VGA 图中的网络具有显著不同的结构特性。

对于研究人员和设计师来说，通常需要比较不同的建筑或设计，例如，比较对特定城市或建筑进行干预的不同设计方案。VGA 分析的彩虹色谱被用于将可视域分析生成的数值数据，在建筑物平面或城市系统上进行可视化。对于整合度，这样的表达方式通常将数值缩放到代表最相互分离的值（蓝色）和最相互整合的值（红色）之间。在将空间系统（建筑物、社区或城市）与不同类型的空间系统对比，或与具有不同干预方式的相同类型系统对比的时候，通常需要考虑各个具有代表性的点的整合度值，以检测整体整合度分布的变化。从最早的空间句法文献 [2] 开始，一直存在一种必要性，以找到调整总深度值的方法，适应不同系统的大小（即网络中的总节点数）。最早的调整方式是由希利尔（Hillier）和汉斯（Hanson）提出的基于 D值调整整合度的方法。D 值整合度指标可用于轴线和凸空间分析，以比较不同的城市和建筑空间系统。这可以被扩展到半径计算（仅考虑图的局部部分，而不是图的整体）。鉴于基于这些数值报告的大量实证结果，似乎可以安全地假设它们已经正确地完成了它们所针对的标准化任务。我们没有理由认为使用 D 值公式计算的整合度不适用于基于轴线和凸空间的分析。因此，当特勒（Turner）首次提出 VGA 分析时 [1]，使用相同的整合度公式实现相同级别的标准化似乎是理所应当的。

最近，一些研究成果开始质疑， VGA 分析的情况下，这些标准化的方法是否仍然正确。例如，在研究模型和迷宫的可理解度（直接基于整合度的单独指标）时，张灵珠等表示， “空间句法的研究定义的可理解度指标，对于相关性的出现至关重要，但这在特定的空间系统（例如玩具模型）中并不适用 [3] ”。这表明在某些情况下，可理解度的计算过程中可能出现某些错误，尤其是 VGA 可理解度的特殊情况。回到整合度指标，首先要注意的是，整合度的计算公式与社会网络分析中的标准化邻近中心度有很大的不同 [4]。造成这种情况的一个原因可能是，与社交网络图相比，轴线和凸空间图的结构属性不同。VGA 图的结构特性也再次被指出其不同之处，并且确实可以被认为与社交网络图更加相似。例如，范内斯（van Nes）和亚穆（Yamu）在他们《城市研究中的空间句法简介》一书中提到了聚合系数 [5-6] 与 VGA 存在相关性，而不是与凸空间网络或轴线网络存在相关性。同样，这需要对 VGA 分析网络中整合度指标的作用或合适性进行更深入的研究。

2 文献综述

希利尔和汉斯在《空间的社会逻辑》 [2] 中首次引入了“标准化”的概念。如其所述，这个数学过程的目的是允许在不同大小的系统之间比较数学意义上“总深度”或“状态”的不同值 [4,7]。空间句法中的总深度（此处把空间 i的总深度 T 定义为Ti）是在大小为 n 的系统中从原始节点 i 到所有其他需要关注的节点 j 的所有最短距离 d 的总和，表示从节点 i 到节点 j 的最短距离，则得到公式（1），即系统中节点 i的总深度为：

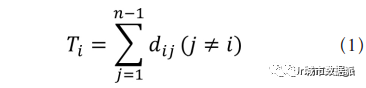
显然，如果图中的节点数量发生变化，那么总深度的值也会发生变化。为此，引入了“平均深度”的概念。对于节点 i 的平均深度表示为，这是总深度与节点总数减一的商。对于平均深度的标准化，相对不对称性将平均深度归一到理论上最小值与最大值之间的数值，适用于不同规模的系统的比较。由此，希利尔和汉斯引入了“相对不对称性”（Relative Asymmetry,RA）的概念，来得到一个介乎最小值和理论上界之间的值，即公式（2）：

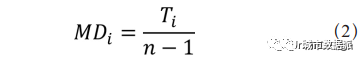
也得到节点 i 的相对不对称性，见公式（3）：

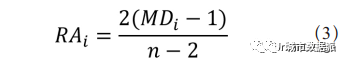
在实践中，真实建筑物和简化为轴线的城市系统往往没有接近理论最大值的最大总深度。为了适应这种现实世界的场景，基于假想的菱形图的上界，被定义为最大深度的上界 [8]。这将得到 D 值的公式，即节点为 n 的菱形图的最大总深度，见公式（4）。

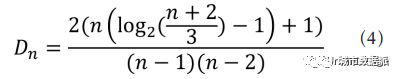
在空间句法分析中使用的值，包括 VGA分析，通常就是标准相对不对称性，即相对不对称性与理论上菱形图的最大总深度的比值。在大小为 n 的系统中，节点 i 的标准相对不对称性值 RRAi 得到公式（5）。

需要注意的是，整合度值就是 RRAi 的倒数。DepthMap [9]和Axman等先前的软件[10]中使用的配色方案倾向于将颜色缩放到地图中最高整合度值（红色）和最低整合度值（蓝色）之间，而不是缩放到从 1 到 0 之间的完整范围。基于整合度的步数深度的变化已被作为大多数形式空间句法研究的支柱，并且所有空间句法软件都对其进行了计算。接下来，我们将考虑空间句法分析中一些不太常用的其他标准化方式。

泰克伦贝格、蒂默曼斯（Timmermans）和范瓦根伯格（van Wagenberg） [11] 批评了希利尔整合度计算方法的不稳定，其在极端情况下无法计算出正常结果。他们还通过比较，以假设的菱形图网络作为比较的基础，借助大量的数值模拟，提出了一种新的方法，对于大小为 L的系统，泰克伦贝格对节点 D 的标准化方法见公式（6）。其中 I 表示标准化的整合度，表示总深度， L 表示节点总数。

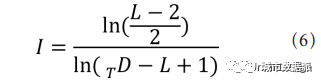
2.2 标准化角度整合度

随着角度指标的引入 [12-13] 和相应的线段分析的使用 [14]，此时便有必要去修改目前“距离”的传统定义，即节点之间距离（要么为零，要么为两节点间的深度整数值，要么为无限大深度），并将其替换为实数（即非整数）值，其通常在 0 和 1 之间。希利尔、杨滔和特勒 [15]接下来引入了标准化角度整合度（NormalisedAngular Integration, NAIN），作为基于线段的系统对中心性进行标准化的新方法，其中表示对于节点 i 的标准化整合度，表示总深度， N表示节点总数。这里应该指出的是，角度、轴线（即未分段）的系统仍然与传统轴线图和凸空间图具有许多相同的基本图形特征。例如，线段的节点度相对较低，其聚类系数的平均值也非常低。由此得到公式（7），即具有 N 个节点的系统中，节点 i 的 NAIN 值。需要注意的是，Ti是从节点 i 出发的总深度，但其通常不是全局的数值。

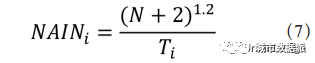
2.3 深度衰减

最后，虽然这不是严格意义上的全局标准化形式，但是两位道尔顿（Dalton） [16] 引入了另一种局部化形式。整合度的众多用途之一是，在使用半径指标时，允许系统的大小不一致。他们的目标是创建一种方法，以允许以更丰富的方式突出局部图形结构，而且使用的是相对较为简便的过程。这里并不是要忽略大于特定步长的深度或半径，例如半径 3(R3)；在深度衰减中，图网络中的这些值仍然得到保留，只不过更远的节点对总深度的增长通过加权的方式被减弱。他们发现，若以 x 为幂，当 x=3.5 的时候，会产生半径为 3 的整合度效果。由此得到公式（8），即对于节点 i 的深度衰减，其中 x 是参数。节点 i 的深度衰减用表示，其中表示从 i到 j 的最短距离， N 表示节点总数， x 表示幂律参数。

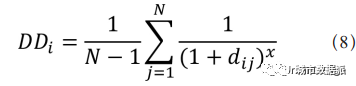
2.4 视线图分析（VGA）

特勒提出了视线图分析 [13,17]，它是基于Benedikt[18] 在 1979 提出的基本空间单位，即可视域发展而来。与空间句法图中通常使用的其他空间表示形式（即轴线空间、线段空间、和凸空间）相比，每个可视域都可以被看作是已有视觉空间的一个样本。特勒观察到，通过任意两个可视域生成位置之间的相互可见性，如前述的空间句法分析，可视域可以很容易形成一个图网络。如果两个可视域生成位置（创建可视域的基础点）可以相互“看到”对方，那么它们在图中就构成了连接，或者边。一旦以这种方式构成了图，就可以很容易地计算出类似中心性的指标，例如整合度。这样，客观的过程就不需要人工手动识别空间，因为所有可前往的空间都可以被可视域生成点组自动“充满”，且该过程可以直接基于包含建筑物墙面的输入数据来实现，而无须任何额外的手动细分。特勒证明了可视域整合度值反映了建筑物中的真实观察结果 [17]。自 2001 年被引入以来，Depthmap [9] 等软件中的 VGA 分析已成为空间句法方法的支柱，特别是对于建筑尺度分析。正如菲尔德（Field） [5] 所提到的，可以将聚类系数与 VGA 结合使用。他们提到，“聚类系数表示一个人从一个位置移动到另一个位置时所损失的视觉信息的多少，更接近凸空间的等视域拥有较高的聚类系数。因此在这些位置上移动时，视觉信息几乎不会丢失”。需要注意的是，轴线、线段角度、凸空间分析不能使用聚类系数，因为该值很接近于零，且任何有意义的值很少会发生变化。这可直接表明 VGA和空间句法中其他所有类型图网络的底层结构是不同的。

最近还出现了一些关于 VGA 的问题。例如，张灵珠、基亚拉迪亚（Chiaradia）和庄宇 [3] 认为，由于不一致的 N 值，可理解度不能很好地应用于可视图。此外，道尔顿等人 [19] 还观察到，VGA 网格旋转角度和原始位置的变化会导致平均整合度值的微小变化。

3 数据和方法

评估 VGA 整合度公式（D 值公式）适用性的理论基础是，对于一个完整的系统，物理空间中一个特定点的整合度值，对网格密度的变化不能过于灵敏。虽然向系统添加更多节点，将会并且应该会增加任何系统的总深度值，但是标准化必须能够消除系统中节点数量的影响。由此可以说，如果我们将可视域的点密度加倍，我们不应该期望在平面图或地图上同一点（即同一位置）的整合度值发生相应的变化。

本文提出的第一个实证实验正是为了做到这一点：在平面图中选择一个点（即位置），并使用不同的、越来越大的点密度的 VGA 重新处理该平面。如图 1 所示，可以在不同的网格密度下处理相同的空间信息，也可以通过选择空间中的点来确定其整合度值会发生什么变化，从而以数值方式检查此过程。为此，可以在每种网格密度下，对离指定位置最近的可视域进行采样并计算其整合度值。

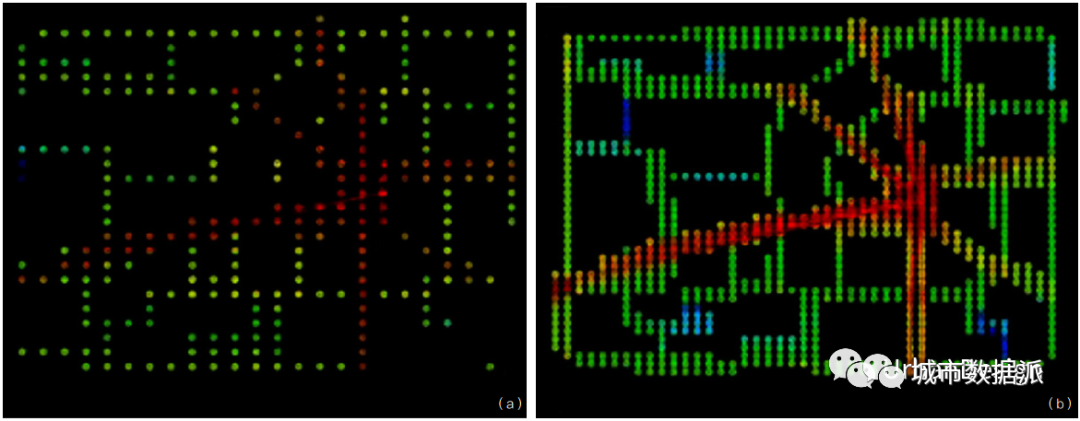
图1 （a）希利尔的可理解世界——网格低密度的一个例子；（b）希利尔的可理解世界——网格高密度的一个例子

然后便可针对一个特定的位置不变的点，构造一个表格来展示其整合度数值与网格大小N（网格点的数量）的关系。很明显，如果整合度数值正常，那么我们会期望看到一条近似水平的直线，代表着近似恒定不变的整合度值（由于实数的数字表达会引起波动，些许噪声是可接受的）。从图 2 中，我们却看到了一条近似反向的曲线。这表明标准化过程还远远没达到对网格大小不灵敏的状态。

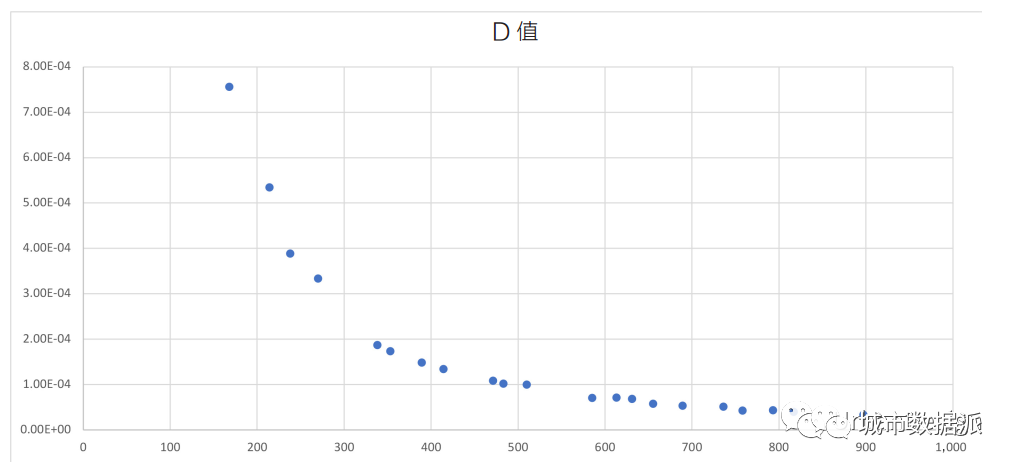
图2 VGA点网格密度变化的过程中，空间中某一位置的D值变化图

对这种实验可能提出的一种批评是，随着网格密度的变化，某些区域的空间可能不成比例地被过分表达或表达不完全。例如，图 1 显示了一个低密度网格。该网格导致右下角附近和左边缘下方的节点缺失。另一个批评是距离指定位置的“最近节点”可能会发生轻微位移，所以我们肯定会看到整合度值微小的变化或波动，因为每次选择的（最近的）点位置都会发生变化。例如，如果“最近的可视域点”与边界相邻或越过边界（例如，在门口的任一侧），我们可能会预料到其整合度值会发生变化。进行这类实验的时候，标准化的过程不一定会发生失败的情况。然而，为了进一步研究这一点，有必要引入视线图分析的一种新方法。

3.1 受限随机视线图分析（R-VGA）

在传统的视线图分析中，首先创建规则正交的网格（即栅格网格），叠加在被分析的区域上 [1]。然后将每一个点都视为一个单元格。它们通常约为 1 米宽（或者为未指定长度的“单位长度”） ，但有时候也不一定。如果网格单元（或栅格点）被“阻挡”，例如落在墙内、落在其他任何实心的无法到达的空间内，则将在分析过程中被移除。从此，每个网格成为计算得到的可视域的中心。接着便可使用热力图的方式对这些计算得到的可视域几何特性进行可视化。像可视域的面积、面积周长比等几何特性 [18] 便可通过这种方式被可视化。此外也可以创建一个图网络来表达可视域与所有其他可视域的关系：如果单元之间（或可视域生成点）彼此相互可见，则把它们连接在一起。这里得到的“图” 便是视线图分析取名的原因。

计算网格间或可视域之间连接的过程不必仅局限于正交网格。我们同样可以使用其他任何类型的网格，例如六边形网格、三角形网格，甚至是基于阿基米德螺线的网格（有关此问题有更全面讨论 [19]）。在探索网格其他形式的时候，有一点立刻变得很明显：我们同样可以通过随机过程来放置可视域生成点。该过程由 Dalton 首次提出 [19-20]。对 Dalton 的可视域点随机放置过程的一种可能的反对意见是，使用随机概率创建可视域生成点，或网格单元，可能会导致创建的点彼此非常接近。因此，对于我们即将展示的随机可视图（random visibilitygraph, R-VGA）的定义，我们对点放置的过程施加了限制。在对点位置随机初始化后，新的点被逐步添加。每次向地图添加一个新的可视域生成点或网格单元时，都会考虑 N 个位置（经过大量实证测试后，选择的值为 N-10）。与标准 VGA 分析类似地，这里每个候选的网格单元都需要事先被检查，以免与任何实心 / 不可达区域重合。每个候选点到系统中已经存在的最近点的距离将被记录下来。在候选点中，与其最近邻近点距离最大的候选点将被选中，并被添加到系统中。该过程将一直持续，直到图中已存在的点的数量达到最大值。这种对初始随机过程的“限制”产生了一个均匀分布的系统（图3），被称为受限随机可视图， R-VGA[19]。

3.2 R-VGA 的计算实验

既然已经对生成受限随机可视图（ 或R-VGA）的过程进行了描述，这时便可回到之前的问题：在网格密度发生变化的时候，提出一个可靠的实验性指标来准确衡量整合度值的变化。如前所述，创建不同密度的 VGA 和R-VGA 图是完全可能的。然而， VGA 分析的网格单元大小的微小变化也可能会导致系统中节点数量的显著变化 [19]。就我们的目的而言，受限随机可视图， R-VGA，相比于 VGA 图的主要优点是，一次只引入一个新的网格单元，而不会影响到现有的已放置的网格单元位置。这将允许使用非常精细的工具来衡量任何与密度相关的整合度值的变化。

因此，可以按以下方式进行第二个计算实验。建筑物 / 区域 / 场地的平面图最初以 125 个完全随机的点作为随机种子。这 125 个随机点将近似均匀分布，并形成骨架、不规则网格或网络。然后可以选择一个网格单元进行研究。在本实验中，选择了 4 个网格单元，一个靠近由传统 VGA 分析计算得到的最高整合度点，一个位于隔绝位置（确定方法与上述方法类似），另外两个位于中间位置（半隔绝和半整合）。然后将一个新的受限随机可视域点添加到系统中。此时再次进行互相可视分析，产生一个新的图（与 VGA 一样），并重新计算这 4 个单元格的整合度值。对于每个选定的可视域，可以绘制出整合度值与系统大小（N，点或网格单元数）的关系图。一旦记录了 4 个整合度值及相应的系统大小，就添加另一个可视域单元，并重复该过程。假设每个单元都处于固定位置，则可以分析深度值的精确变化，而不会因点的放置而产生干扰或噪声。

现已有新的软件专门为该目的进行开发。该软件通过 Java 语言，使用 Processing IDE 和相关的库进行开发 [21]。D 值计算的代码是从DepthMap 的 开 源 C++ 代 码 [22] 中 的 PafMath.h文件直接转移到 Java 中而得到，以避免任何转录或重新编码错误。有几个环境在此过程中被处理。下面显示了一个测试环境示例。它有 4个选定点。这是希利尔的可理解世界（图 3）[23]。

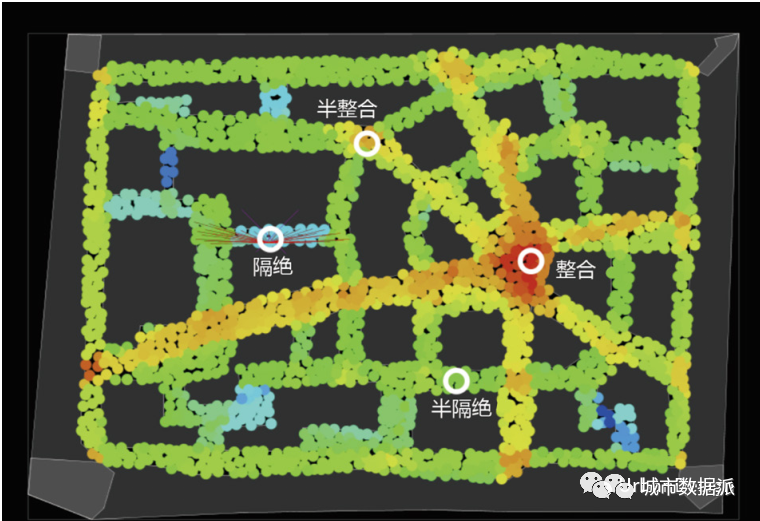
图3 对希利尔的可理解世界示例采取R-VGA的方式进行处理。该图展示了网格单元的位置

4 结 论

4.1 希利尔和汉斯基于 D 值的标准化

在图 4 中，纵轴显示了每个位置的整合度值，横轴显示了系统的大小（在本例中为125 到 2000 个可视域）。首先，该图证实了图2 中增加标准 VGA 网格密度的结果。除此之外，它还显示出更多的规律性和更少的差别。需要注意的是，整合度值都非常低，范围在0.004,730,009 到 0.000,008,438,05 之间。鉴于大多数形式的标准化目的是对值进行归一化以便于比较，这些极低的值可能表明，这些整合度值（基于 D 值公式）不适合这种形式的图。

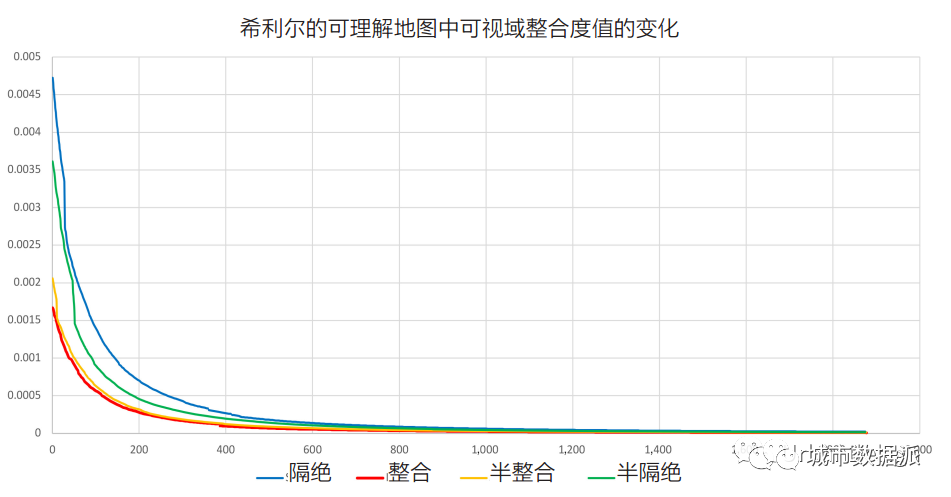图4 被选中的4个网格单元的整合度值图

从好处来看，这张图和其他图表明，虽然整合度的绝对值发生变化，但是被选中的 4 个点的整合度值的排名顺序从未改变，并且 4 个值之间的比率实际上也是恒定的。这可以通过查看在给定网格单元数 N 的情况下，一个整合度值与最整合的点的整合度值的比率来评价。通过查看所有 N 的计算结果的比率，同样可以从平均值中衡量出标准差。这个过程表明，比率最多只有 6.5% 的变化。鉴于许多 VGA 图仅通过目视观察，其颜色和数值分布保持着一致性（人眼很难检测到 6.5% 的颜色变化）。这种比率的一致性也可以解释为什么以前使用 VGA工具的研究人员对整合度值的变化感觉不明显。虽然整合度值的差异保持不变，但是整合度和大多数应用中的 D 值（特别是对于非 VGA 分析）没有受到影响。而在比较具有不同 N 值的不同VGA 图的时候，情况就会有所不同。

回到图 4，整合度值的变化整体来看非常平滑。其中唯一显著的变化是添加了一个网格单元可视域。这导致在图中形成了一个新的“视觉捷径”，从而降低了系统的总深度。对于希利尔的可理解世界，在这种布局下，网格单元达到 400 个（N=400）以后，系统变得完全饱和。一旦达到饱和，我们可以再次确认，虽然整合度的相对值保持不变，但是它们的绝对值发生了变化。从这个实验中，我们可以得出结论，使用 D 值公式进行整合度标准化的过程，无法消除系统大小的影响。这与其在轴线图中的表现有所不同。为了深入了解为什么这不起作用，我们可以查看 K 的值，即可视域网格单元的连通性：最整合的网格可视域的连通值范围从 K=21 (N=125) 到 K=408 (N=2000)。这些都远高于典型的城市或建筑尺度的轴线图中的结果。换句话说， VGA 可视域图是非常不一样的图。

4.2 特克伦堡标准化

对于前面章节中介绍的其他形式的标准化，可以重复类似的过程。同样，为了确保一致性，计算代码从原始 DepthMap 代码 [22] 转移到 Java。图 5 显示了相同的 4 个位置的类似图。其使用了特克伦堡、蒂默曼斯和范瓦根伯格提出的另一种标准化形式 [11]。最初的标准化过程是为轴线图和节点图设计的。从图 5 可以看出，这些值也随着系统规模的变化而不稳定。根据图表，读者可能会认为，相比于上面的整合度示例，这些数值更为不连续。应该注意的是，在图 5 中，图表的轴从 0.6 开始。与整合度的示例相比，其夸大了差异。

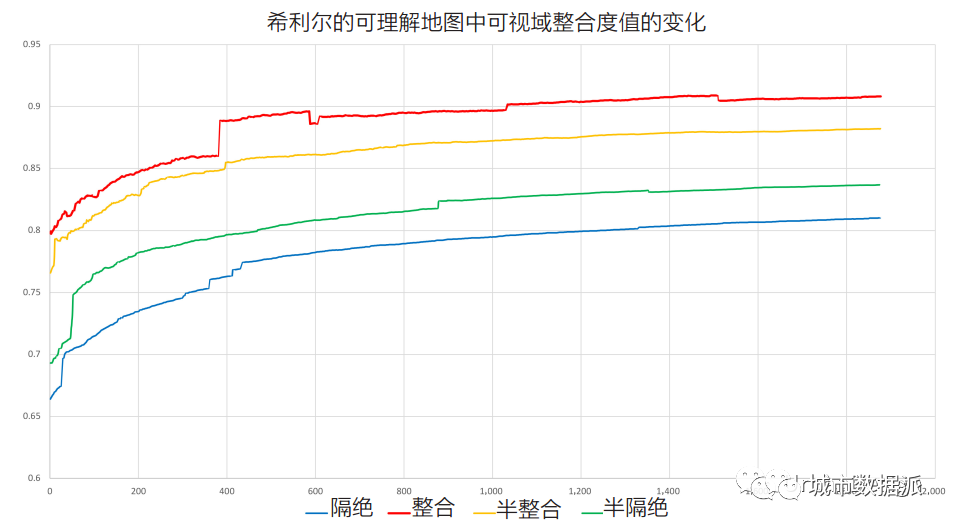
图5 被选中的4个网格单元的Teklenburg相对化结果图

根据图 5，我们可以看到在 VGA 和 R-VGA的情况下，这种出色的标准化形式，也打破了一些基本假设。这不应被视为对特克伦堡等人标准化过程的批评，因为它们最初是为完全不同类型的图而设计的。然而，从该图中可以明显看出，将含有 400 个可视域的系统与含有1,800 个等视域系统的特克伦堡整合度绝对值进行比较，会导致错误的结论，即整体来说，更密集的系统整合程度更高。

4.3 标准化角度整合度（NAIN）

我们的软件也可以进行标准化角度整合度（Normalised angular integration, NAIN） 这 种标准化的方式。下面的图 6 显示了相同 4 个位置的计算结果。

图6 被选中的4个网格单元的NAIN相对化结果图

由图 6 可看出，对不同大小的系统而言，这些值之间也不能真正进行比较。由此可以得出结论，对于 VGA 和 R-VGA 类型的图，这并不是在不同系统大小之间进行标准化的有效方法。对此的基本解释是， VGA 和 R-VGA 再次打破了关于图结构的基本假设。它们与轴线、凸空间或线段图关于图的假设有所不同。可视图是完全不同类型的图。

4.4 深度衰减标准化

最后，我们看看深度衰减标准化 [16]。这从未被认为是另一种寻找标准化过程的尝试，而是一种把计算不同半径的过程泛化的方法（类似于常用的轴线分析中使用半径的方式）。深度衰减通常会尝试比较同一地图中的不同区域，因此基本上忽略了系统的大小。为了完整起见，值得另外研究使用深度衰减指标来比较VGA和R-VGA。从图 7 可以明显看出，在使用 R-VGA（以及 VGA）的情况下，面对不同大小的系统，深度衰减也并没有让整合度值保持不变。

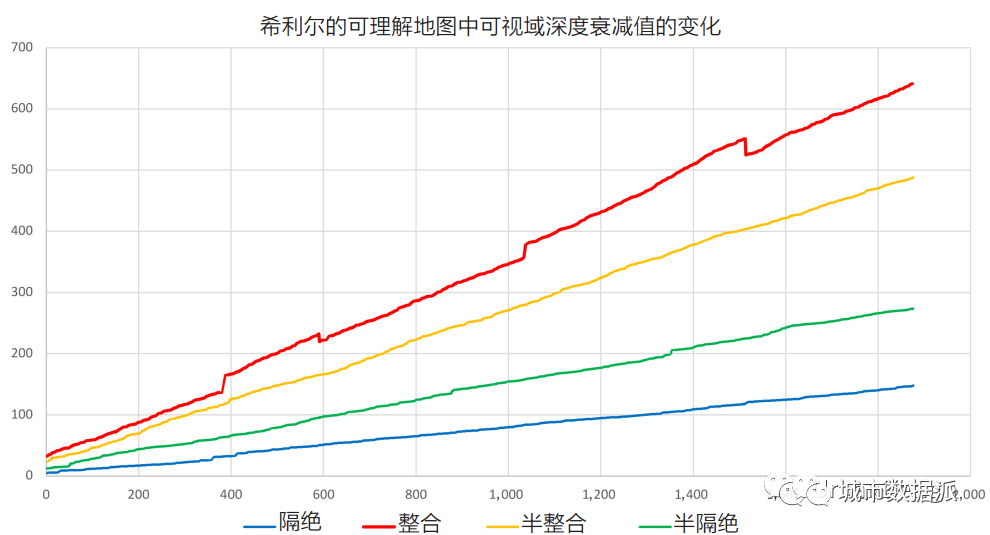
图7 被选中的4个网格单元的深度衰减相对化结果图

4.5 VGA 标准化黄金法则的提出

正如我们所看到的，上面介绍的任何一种标准化方法似乎都不能在不同的尺度上（可视域点数量）产生数值上可靠的结果。这就引申出一个问题，即如何使研究人员能够比较不同大小的空间系统中不同的整合度值。本文提出两种方法来解决这个问题。

第一种方法是基于我们新的受限随机视线图分析（R-VGA）。如前文所述，传统 VGA和新的 R-VGA 方法之间的主要区别在于，能比较容易引入固定数量的网格单元。实际上，网格单元的总数必须被指定，以给被逐个放置的每个网格单元提供一个阈值点。通过调整网格密度来实现特定数量的网格单元，对于标准VGA 而言是一项挑战。一个简单直接的解决方案是为所有系统选择固定数量的网格单元。通过使用相同数量的单元，最简单形式的“总深度”便可直接用于比较总深度值，而无须任何类型的标准化。如果该固定的数字足够大，且完全覆盖系统，则可以直接比较总深度。这应该被视为一个“黄金法则”。我们可以通过它来考虑其他标准化过程。

4.6 新的标准化方法的提出：上界标准化（Upper-bound Relativisation, UBR）

最后，我们介绍了一种新的标准化过程，专门为类似于 VGA 和 R-VGA 的图 / 网络而设计。如果对系统的总深度值（y 轴）与系统大小（x轴）绘制图表（图 8），可以看出，相对于系统大小，曲线大致呈线性增长。从这个角度来看，一种简单的标准化形式是将总深度 D 除以系统的大小（类似于平均深度的计算）。

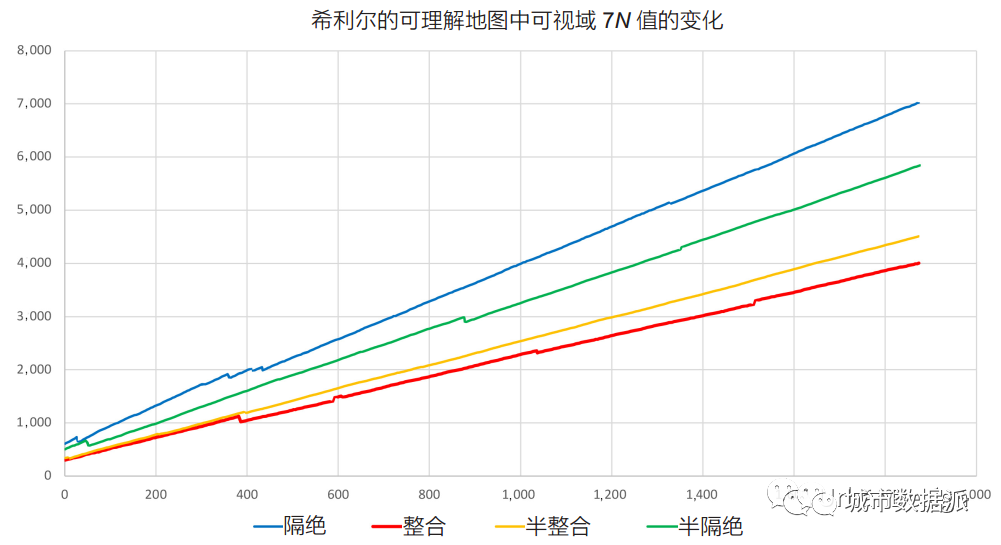
图8 被选中的4个网格单元的总深度

在实践中，这会产生介乎 1 到 6 之间的数字。因此，从实验的角度看，我们除以 (7*N)以获得更接近 0.0 到 1 范围的数字。

执行了这一步后，从图 9 中可以看出，我们期望从 UBR 标准化中获得各种结果。观察图表的右半部分，我们发现这些值是相对恒定的，表明标准化过程是正确的。对于拥有大于 500个网格单元的系统，这些值大致是恒定的，正如我们对于正确完成标准化的系统所预期的那样。对于大于 500 个可视域的系统， UBR 的所有值的标准差趋向于最多 0.023,925,5，即只有1.64% 的偏差。对于包含少于 500 个可视域的系统，其发生的变化中大部分可以用总深度的突然且微小变化来解释。在新的可视域点的放置让图网络产生新的视觉捷径的时候，这种变化一般就会发生。我们将这种现象称为“连接跳跃”（另请参阅我们的论文，特别是关于“连接跳跃”和“惊喜时刻” [24]）。对于少于 500个可视域的系统，其总深度值确实发生了变化。但我们可以说这只是反映了其往“正确值”的逐渐逼近，并且是因可视域数量少而引起的噪声。因此，我们可以自信地指出， R-VGA 应该从最少 N=500 个可视域开始。但是对于更复杂的系统而言，其可能需要更大的值。应该注意的是，对于值域在 0.0 到 1.0 之间的 UBR 值，理论上可能会出现值大于 1.0 的高度被隔绝的位置，但其在日常使用中极不可能出现。

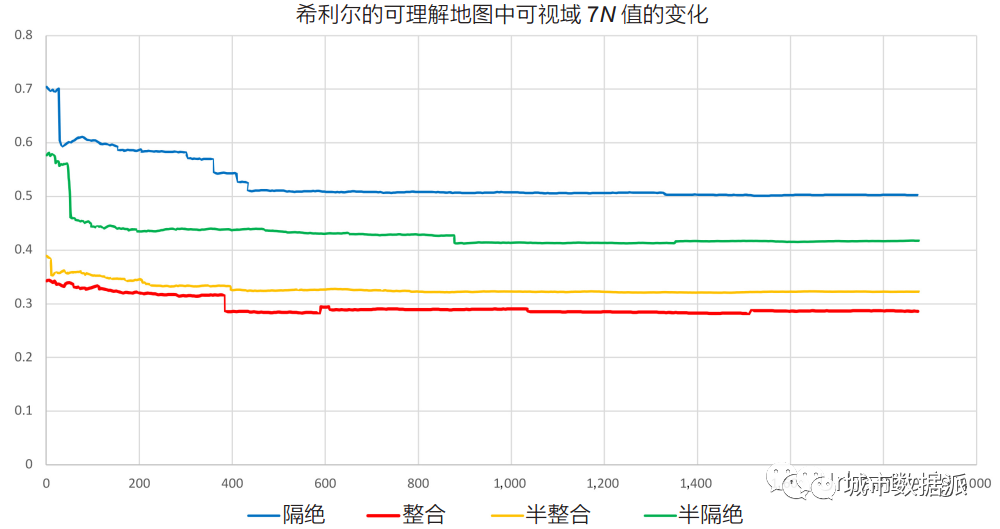
图9 被选中的4个网格单元的UBR相对化结果

5 讨 论

从图 3—图 9 中进行和呈现的计算实验中可以看出，不管是 VGA 分析还是 R-VGA 分析，现有的标准化过程（D 值公式）无法实现在不同大小的系统之间进行公平的比较。我们相信，如果拓扑指标（D 值公式存在的目的）能被用于对轴线图或凸空间图进行类似的实验，标准化过程将如预期的那样被正确实现。前述的一些通用方法已被应用于各种不同的图中。这些方法通过全局和局部的半径指标，对各种建筑物、各类城市住区进行比较。而假定这些方法能被直接完美地迁移到可视图中，是不合理的。如 VGA 和 R-VGA 的情况所示，整合度值似乎不允许系统的大小发生变化。这与对轴线图进行相同的实验时所预期的一样。之所以会出现这种问题，是因为 VGA 和 R-VGA 创建的图与轴线图和凸空间图具有不同的内在结构特性。具体来说， VGA 和 R-VGA 表现出高水平的聚类系数，而轴线图和凸空间图则不是。

聚类系数用于衡量局部的互连性，其在许多社交网络中较为常见。对于社交网络，如果节点（人） A 与节点（人） B、节点（人） C 相连，那么（人） B 和（人） C 之间很可能也存在联系。聚类系数介于 0 和 1 之间。0 即意味着没有互连（第一级连接中没有任何邻接点）；1 即意味着节点 A 的每个邻接点都与其他所有邻居相连。轴线图和凸空间图通常表现出非常低的聚类系数值（值范围介乎 0 和 0.1 之间）。此处介绍的实验使用了密集 VGA 和 R-VGA 图。它们产生的聚类系数值接近于希利尔的可理解世界的 0.7 和新加坡购物中心的 0.78（另一个已分析但未在此处展示的世界）。我们认为，图中这样或那样的结构差异，否定了该领域先前工作中已有的基本假设 [2, 11, 15]。

当需要比较不同的系统时，尤其是不同大小的系统时，本文已提出了替代的方法来实现这一点。第一种方法就是在两个系统中都使用相同的可视域数量进行 R-VGA 分析。如果可能的话，可以用传统的 VGA 来完成。但是如前所述，这非常困难，因为用户在 Depthmap 中几乎无法对网格布置的这一方面进行控制。反复试验将是实现这一目标的唯一机制。而 R-VGA 简化了流程，因此这种时候建议使用它。同样，R-VGA 分析还有其他优势。在我们的另一篇论文 [19] 中对此进行了拓展。而本文提出的第二种方法是 UBR，可以作为标准化的一种相对简单的形式。这将允许使用本文提出的新 UBR 值进行系统间的比较。

6 总 结

最早，标准化一直都是空间句法研究的一部分 [2]。很长时间以来，它一直允许不同类型的轴线空间和凸空间之间进行比较。它已在各种不同的背景下得到运用，并成为空间句法本身的让大家很熟悉的部分。本文证实了，通过研究不同密度的可视域网格的系统，标准化过程似乎没有像最初设想的那样进行，特别是对于 VGA 和R-VGA 图。但是这不会对先前的研究构成任何质疑，因为对于大于 2,000 个节点 / 单元的系统，值域在 2,000 到 3,000 之间的整合度值里，值之间的差异不会发生显著变化。

然而，从理论的角度来看，当之前的标准化机制被专门应用于 VGA 和 R-VGA 图时，我们确实对绝对可靠性提出质疑。应该注意的是，对其在最初被设计出来时从未考虑的情形，现有的标准化机制将变得不可靠。

本文提出了两种不同的标准化机制。第一种方法是使用受限随机可视图， R-VGA，其使用相同数量的网格单元或可视域来分析系统。如果选择的值足以（超过 500 个可视域）对全部空间构造出密集的模型，那么总深度值之间将可直接进行比较。第二种方法，我们称为UBR，是专门为 VGA 和 R-VGA 系统定制的标准化过程。应该注意的是， UBR 并不是为了成为通用的标准化过程而被提出的，它是专门为类似于 VGA 和 R-VGA 的系统而设计的。UBR系统与对应图结构的相互协调关系，就像整合度或 NAIN 与轴线图和凸空间图的形式特征之间的关系那样。

本文主要的贡献在于 UBR，一种用于直接比较不同大小系统之间整合度值的方法。此外，本文还提出了替代的解决方案——进行 R-VGA分析的时候使用固定大小的系统。这种方案可用于继续研究这种更深层次的理论分析。如果把固定大小的 R-VGA 图当作标准方法，则空间句法社区必须就特定大小的 N 达成一致，例如 N=1,000 用于小型房屋和建筑物， N=5,000用于大型建筑物， N=10,000 用于社区等等。第三，许多研究人员一直试图使用 VGA 可理解度指标。但是由于众所周知的问题，研究人员都避开了它。VGA 可理解度的问题可能仅仅源于整合度公式应用在 VGA 图上的时候公式所产生的问题。因此，固定大小的 R-VGA 图，或应用于 VGA 的 UBR，均可让 VGA/R-VGA可理解度指标的正确使用得到保证。最后，本文还开发了一种方法，用于在不同版本和分析迭代中，追踪空间中固定点的可理解度值。这也为空间句法方法知识库做出了独特的贡献，为未来的研究人员提供了方法，以给类似 VGA的系统验证不同标准化的形式。

参考文献

[1] Turner A,Doxa M,Sullivan D,et al.From isovists to visibility graphs: A methodology for the analysis of  architectural space [J]. Environment and Planning B,  2001, 28(1): 103-122.

[2] Hillier B, Hanson J. The social logic of space [M]. Cambridge: Cambridge University Press, 1984.

[3] Zhang L, Chiradia A, Zhuang Y. In the intelligibility maze of space syntax: A space syntax analysis of toy models, mazes and labyrinths [C]. Proceedings of ninth international Space Syntax Symposium, Seoul: 2013.

[4] Bavelas A. Communication patterns in task-oriented groups [J]. The journal of the acoustical society of America, 1950, 22(6): 725-730.

[5] Van N A,Yamu C. Introduction to Space Syntax in Urban Studies [M]. Heidelberg: Springer, 2021.

[6] Watts D J, Strogatz S H.Collective dynamics of “small-world” networks [M]. Oxford:Nature, 1998, 393(6684): 440-442.

[7] Harary F.Graph theory [M]. Bolder: Westview Press, 1994.

[8] Kruger M.On node and axial grid maps: Distance measures and related topics [C]. European Conference on the Representation and Management of Urban Change, Cambridge: 1989.

[9] Turner A.Depthmap 4: A researcher’s handbook[R].London:University College London, 2004.

[10] Dalton N. An advanced tutorial in axman software manual produced by the space syntax laboratory [R].London:University College London, 1997.

[11] Teklenburg J, Timmermans H, Wagenberg V. Space syntax: Standardised integration measures and some simulations [J]. Environment and Planning B, 1993,3(20): 347-347.

[12] Dalton N. Fractional confgurational analysis and a solution to the Manhattan problem[C]//Proceedings of the3rd International Symposium on Space Syntax.Atlanta, 2001: 26.

[13] Turner A. Angular analysis[C]//Proceedings of the 3rd International Symposium on Space Syntax. Georgia Institute of Technology, Atlanta. 2001: 1-11.

[14] Hillier B,Iida S.Network and psychological effects in urban movement[C]//Proceedings of the 2005 international conference on Spatial Information Theory. Elliottville, NY. 2005: 475-490.

[15] Hillier B,Yang T,Turner A.Normalising least angle choice in Depthmap-and how it opens up new perspectives on the global and local analysis of city space [J]. Journal of Space Syntax, 2012(2): 155-193.

[16] Conroy-Dalton R,Dalton N.Applying depth decay functions to space syntax network graphs [C].Proceedings, 6th International Space Syntax Symposium. İstanbul, 2007.

[17] Turner A,Penn A.Making isovists syntactic: Isovist integration analysis[C].Proceedings of the 2nd International Symposium on Space Syntax. Brasilia,1999.

[18] Benedikt M L.To take hold of space:isovists and isovist fields [J]. Environment and Planning B, 1979,6(1):47-65.

[19] Dalton R, Dalton N, McElhinney S, et al. Isovists in a Grid;benefts and limitations [C]. Proceedings of the 13th Space Syntax Symposium.Bergen, 2022.

[20] Dalton N.Synergy, intelligibility and revelation in neighbourhood places [D]. London:University College London, 2011.

[21] Arnold K, Gosling J,Holmes D.The Java programming language [M]. Massachusetts: Addison Wesley Professional, 2005.

[22] Turner A,Varoudis T. DepthMap [R]. London:University College London, 2012.

[23] Hillier B.Space is the machine [M]. Cambridge: Cambridge University Press, 1996.

[24] McElhinney S, Dalton R, Dalton N, et al. Detection of intelligibility leaps using Isovist-waves;joining the dots to map potential “aha moment” locations [C].Proceedings of the 13th Space Syntax Symposium. Bergen, 2022.

作者简介：

尼克·S·道尔顿（副教授，英国纽卡斯尔诺森比亚大学）

露丝·道尔顿（教授，英国兰卡斯特大学）

山姆·麦克尔希尼（副教授，英国创意艺术大学）

帕纳吉奥蒂斯·马夫罗斯（博士、研究员，新加坡和苏黎世联邦理工学院联合中心未来城市实验室）

[译者]邓成汝（规划师，中规院(北京)规划设计有限公司）

通讯作者：Nick S.Dalton；

E-mail: nick.dalton@northumbria.ac.uk。

参考文献引用格式：

[1]尼克·S·道尔顿,露丝·道尔顿,山姆·麦克尔希尼, 等.上界映射与随机可视域：对比视线图分析系统的解决方案[J].城市设计, 2022(5): 56-71.

Dalton N S, Dalton R, Bhinney S M, et al. Upper Bound Projection and Stochastic Isovists: A Solution to the comparison of visibility graph analysis systems [J].Urban Design, 2022(5): 56-71.