

1
内容导读

在空间上,相似地理现象的分布可能有两种模式。第一种模式如地理学第一定律所述,邻近的地方有着相似的地理现象,例如距离较近的气象站可能会观测到相似的天气。与此同时,相似的地理现象也可能出现在不同的地方,例如意大利南部和美国加州地区都属于地中海气候。这种“相似的地理现象既可能出现在邻近的地方,也可能在相隔甚远的地方重复出现”的地理分布模式在现实世界中很常见。
对这种分布模式的发现和描述,可以概括为“复现地理模式发现”问题(repeated geographic pattern discovery, RGPD)。这种地理模式有两个特点:(1)同一种地理现象可以在空间中的不同地区重复出现;(2)该地理现象在一个地区出现时保持空间连续性(表现为空间自相关性)。事实上,大多数地理现象都可以从“复现性”和“空间连续性”两个角度来衡量。
空间聚类算法可以将不同的地理区域根据其属性或者空间关系分割为多个空间邻近区域。然而,传统的空间聚类算法在解决“复现地理模式发现”问题时可能会面临挑战。传统的空间算法可以划分为三类:(1)基于属性的空间聚类;(2)基于密度的空间聚类;(3)基于区域化(regionalization)的空间聚类。基于属性的空间聚类一般将空间关系(如坐标点)作为属性输入,但会欠缺对空间连续性的考虑。基于密度的空间聚类虽然能够发现空间上聚类的分布,较好地保留了空间连续性,但却无法解决空间上聚类的“复现性”问题,也就是说,两个本应属于同一类型的聚类,会因为在空间上被其他聚类隔离,而被视作不同的类型,故而难以发现在空间上复现的地理现象。基于区域化的空间聚类将空间划分为不同的区域,同样能保持空间连续性,但每一聚类的都被视作不同的类型,因此也难以发现复现的地理现象。
图1 显示了不同类型空间聚类算法的一种可能的输出结果。图1(A)中,拥有着相似属性的不同区域可以被基于属性的空间聚类发现,但空间连续性可能被破坏;图1(B)中,空间被分割为5个区域,空间连续性被较好地保留,但是属性相似但相互隔离的场所难以被发现。我们则提出一种新的空间聚类算法——STICC,全称为“基于托普利兹逆协方差的空间聚类” (Spatial Toeplitz Inverse Covariance-Based Clustering),用于发现空间中虽相隔但又属性相似的场所,同时保持空间连续性,其可能的输出结果如图1(C)所示。
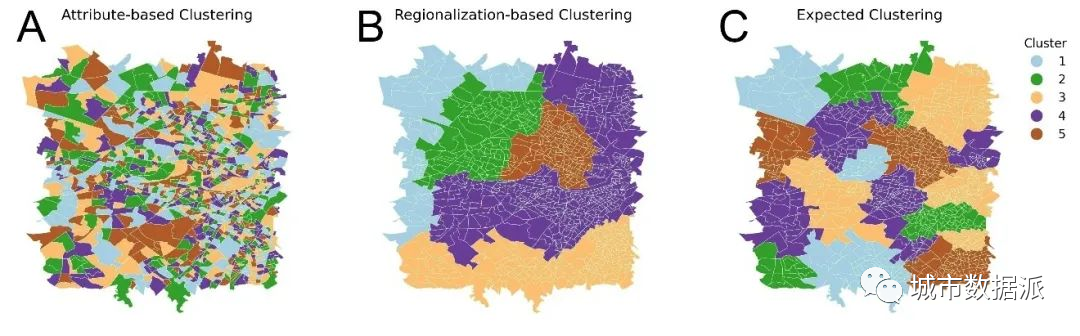
图1 不同类型空间聚类算法的可能输出结果
图2显示了不同空间聚类算法所适用的地理现象在“复现性”和“空间连续性”两个维度上的分布。
为了能发现属性相似的场所/地方,同时保持空间连续性,STICC算法有两大特点:
(1)我们构建了子区域(subregion),在聚类时将中心地理对象和其邻近对象一起考虑;
(2)我们采用了一种“空间一致”(spatial consistency)的策略,让邻近的地理对象尽量归属于同一聚类。
本文算法灵感来源于2017年KDD会议最佳论文TICC算法。原算法适用于多变量时间聚类问题,然而多变量时间聚类与多变量空间聚类不同,因为前者有顺序,而后者无顺序。
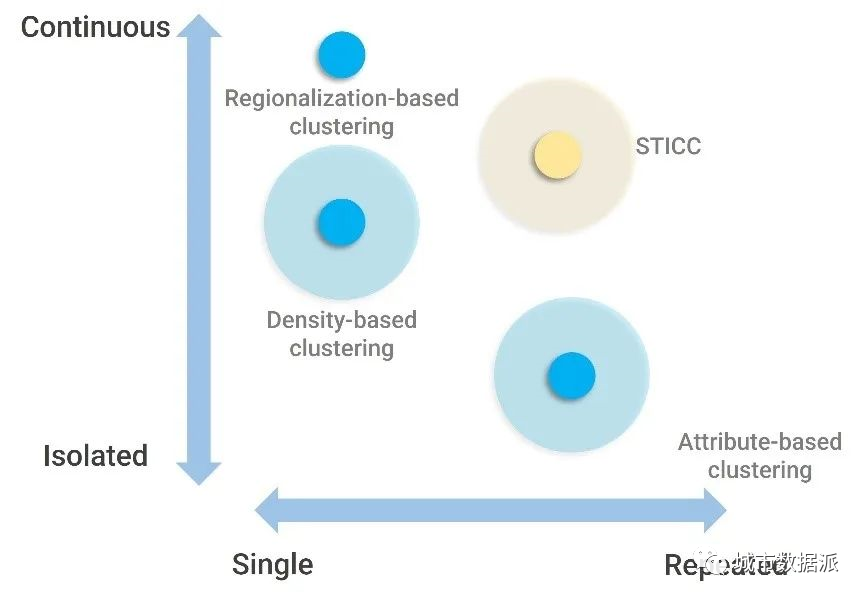
图2 不同类型空间聚类算法所适用的地理现象在 “复现性”和“空间连续性”两个维度的分布
2
算法思路

图3介绍了STICC算法的基本思路。如图3所示,空间中可能存在A(红)、B(蓝)和 C(绿)三种聚类,其中聚类A在不同的区域复现出现。每一个地理对象(图3中为点)包括了D维变量(图3中D=6)。对于每一个地理对象,我们首先以其为中心地理对象,构建一个子区域(subregion),其半径能让该子区域包含R个地理对象,包括中心地理对象本身和其最近的R-1个地理对象。对于每个聚类,我们用一个马尔科夫随机场(Markov random field, MRF)来表达其结构。该随机场有R层,每一层有D个节点。各个节点之间相互连接,这些连接的边可以用来表示同一个地理对象不同属性间的关系,以及同一个子区域内不同地理对象的不同属性间的关系(以下简称为“地理对象属性间关系”)。
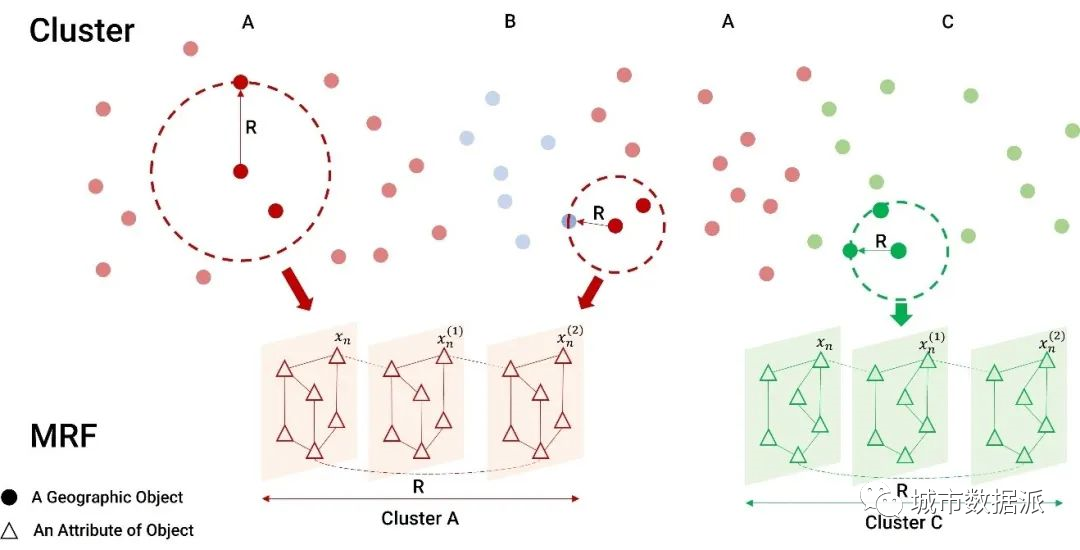
图3 STICC算法思路:图中有A, B, C三个聚类,子区域的“半径”R=3,每个地理对象有6个属性,MRF中连接各节点的边代表了子区域内地理对象属性间关系
由于不同聚类的属性和空间依赖不同,故而,不同聚类的MRF不同。
为了习得各个聚类的马尔科夫随机场参数,我们定义了如下的优化目标公式。与此同时,我们使用了托普利兹矩阵来表达每个聚类中地理对象属性间关系,通过学习各个聚类托普利兹矩阵的值,最终可以确定各个聚类的MRF,从而计算出各地理对象的聚类结果。当托普利兹矩阵的值(即地理对象属性间关系)结果收敛,则聚类算法结束。优化目标如图4所示:

图4 优化目标公式
3
算法实验

我们将STICC和其他一些较为常用的算法,如K-Means、DBSCAN、GMM以及ArcGIS中的空间限制多元聚类算法等,在模拟数据集和现实世界签到数据集上进行了对比。为了评估不同聚类算法的性能,我们使用了调整兰德系数(Adjusted Rand Index, ARI)、Macro-F1分数和Join count statistics。前两者可以用于评估聚类的准确性,而Join count statistics可以评价空间连续性是否在一定程度上得以保留。
图5为生成的模拟数据集。其中包括10个区域和7种聚类类型。由于已经知晓各个点所属于的聚类,故可以评估准确性。图6结果显示,STICC在三个指标上,在精度和空间连续性两个方面都取得了较大的领先。
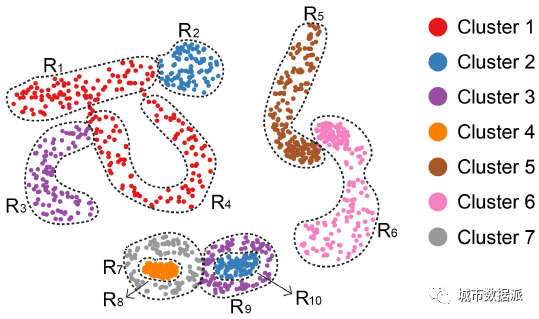
图5 模拟数据集
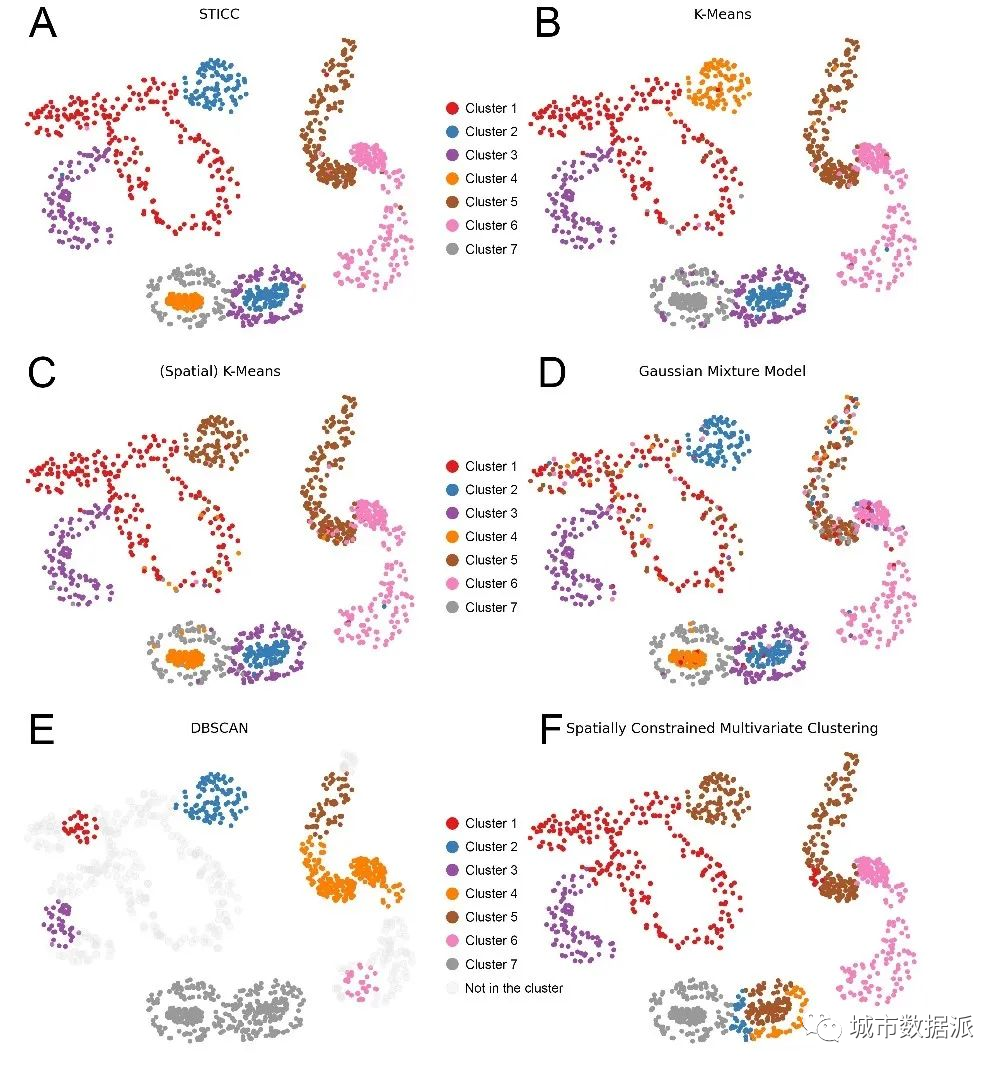
图 6 不同算法在模拟数据集的结果
我们还在一个真实世界签到数据集上进行了测试。该实验的任务为基于签到时间(仅包括小时和星期)来聚类POI的类别。其中包括二分类(工作地、居住地)和三分类(工作地、居住地、健身场所)两种划分方法。图7为部分签到数据聚类结果。结果显示,STICC在三个指标上取得了较大的领先。
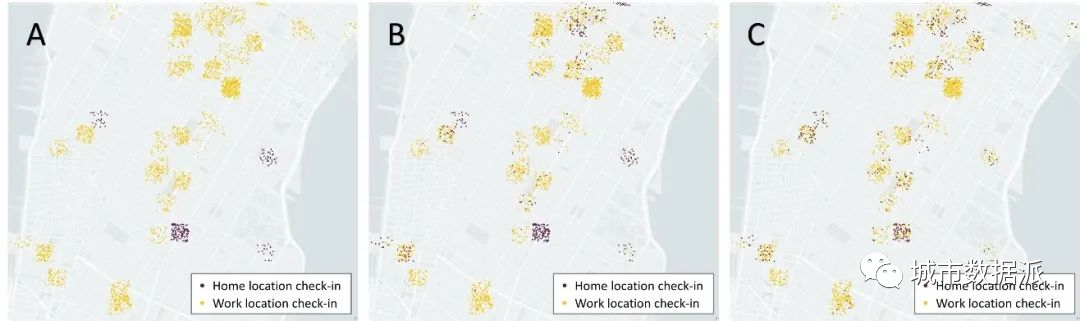
图 7 签到数据聚类结果:(A)真值;(B)STICC结果;(C)K-Means结果
4
总结

本文提出了一种基于托普利兹逆协方差的空间聚类算法——STICC。该算法考虑子区域,并采用一种“空间一致”策略,从而较好地适用于解决 “复现地理模式发现”问题(repeated geographic pattern discovery, RGPD),即发现互相隔离但属性相似的地理模式,并保留空间连续性。该算法将空间思维与人工智能算法有机结合,为空间显式模型的发展提供了新思路。未来,该方法或能适用于社会、地理、经济、交通等多项应用中。
当然,STICC也存在一定局限性。例如,STICC需要人为设置多个参数,包括聚类个数、空间一致惩罚系数、子区域大小等。在未来的研究中,我们将会更加细致地评估不同参数对于STICC算法性能的影响。
本文所有代码和数据已经开源在 https://github.com/GeoDS/STICC.
5
参考文献

Yuhao Kang, Kunlin Wu, Song Gao, Ignavier Ng, Jinmeng Rao, Shan Ye, Fan Zhang & Teng Fei (2022) STICC: a multivariate spatial clustering method for repeated geographic pattern discovery with consideration of spatial contiguity, International Journal of Geographical Information Science, DOI: 10.1080/13658816.2022.2053980
素材来源:S³-Lab
材料整理:康雨豪、叶山
内容排版:张维昱

原文始发于微信公众号(城市数据派):【空间显式模型新思路】一种发现复现地理模式的多变量空间聚类算法丨城市数据派
 规划问道
规划问道







