盛志前 | 基于通勤大数据的出行空间分布模型测评与改进

在工程领域广为应用的四阶段交通需求预测模型中，重力模型通常被用于预测出行的空间分布。重力模型最早是受物理学中的万有引力定律启发而提出的一个先验模型，在得到实际出行调查和统计数据验证后在实际中应用。重力模型假设p地至q地的出行量g_pq与p地的产生量O_p、q地的吸引量D_q成正比，并随两地间阻尼(通常以距离、出行时间、费用等表征)增加而减少。以阻尼函数f(u_pq)表达g_pq随两地间阻尼(u_pq)增加而衰减的量度，即g_pq正比于f(u_pq)，f(u_pq)为u_pq的减函数。在出行者目的地选择问题的场景下，基于统计物理中的最大熵原理——系统最可能出现的出行分布是微观状态数最多的分布(最可几分布)，A. G. Wilson^[1]提出了一种从最大熵原理导出重力模型的方法。受益于A. G. Wilson^[1]的工作，采用负指数形式阻尼函数的熵模型受到广泛关注，在该模型中两地间出行量g_pq正比于，γ为需要标定的参数。最大熵原理仅能给出系统最可能的宏观分布状态，却没有考虑系统中出行者选择目的地的微观决策过程。M. E. Ben-Akiva 等^[2]从个体决策行为角度建立了随机效用离散选择模型，即著名的Logit模型，并证明了重力模型可以从Logit模型导出，从而为重力模型提供了微观经济学解释。这些理论研究^[1-3]进一步巩固了重力模型在实际应用中的地位。交通工程师在实际工作中发现采用乘数阻尼函数(即，其中α，β为需要标定的参数)的出行空间分布模型能更好地适应出行调查数据的形态，这种形式的出行空间分布模型被称为广义重力模型。

针对不能获取翔实的出行数据的情形，F. Simini 等^[4]提出了一个无须调查数据标定的出行空间分布模型，称之为辐射模型。在该模型中，g_pq不仅与p，q两地的出行参数相关，还与以p为圆心、以p至q间距离为半径的范围内所有分析单元的出行参数相关，以体现个体在选择目的地时的竞争效应。闫小勇^[5]进一步放宽了辐射模型的假设条件，提出了与辐射模型类似的出行空间分布模型，即人口权重模型。这一类模型继承了介入机会模型^[6]的重要思想，即：用排序而不是精确计量的阻隔来衡量各目的地距离起点的远近，从而尽可能减少分布模型对于实际出行数据的依赖。然而，在信息化背景下，大量出行数据可以通过互联网位置信息轻易获取，这一类模型最主要的优势也就丧失殆尽。另外，是否存在能够用于各种土地利用状态的普适的出行空间分布模型本身就存在争议。基于以上原因，这类模型在实际中没有获得广泛应用。

另一种在工程领域较为常用的出行空间分布模型为增长率模型，以Fratar模型为典型代表。模型的基本假设是出行空间分布形态在未来保持不变。Fratar模型在用于预测时需要基准年完整的出行OD数据，还要求研究区域土地利用形态、交通设施服务水平等基本保持不变。如果现状两个交通小区间出行量为零，那么未来年预测量也一定为零。这些都限制了Fratar模型在出行空间分布预测中的应用。

综上，由于相对于其他模型的比较优势，重力模型被广泛研究并用于城市的出行空间分布预测中。由于成本、时间周期等限制，标定重力模型的出行调查数据通常只有很小的样本(百万人口以上的城市，出行调查的样本量通常为1%~3%)。由于缺乏较大规模样本的实际出行数据，重力模型对于城市实际出行分布的重现能力一直没有得到评价。近年来得益于信息化技术的发展，关于出行的信息化数据逐渐出现并得到应用^[7]。地图位置服务和移动通信运营商手机信令数据均可实现对通勤者居住地和就业地的识别^[8]。通过大数据获得的城市中心城区通勤OD达到通勤人口的80%以上，基本上覆盖了所有具有稳定居住地和就业地的通勤人口^[9]。这为重力模型的评价建立了数据基础。

本文采用一个城市实际的交通网络和通勤大数据，以工程领域广为应用的双约束重力模型为例，测试传统出行空间分布模型对通勤出行样本量的敏感性以及在不同尺度上对实际通勤空间分布的重现能力，揭示出行空间分布模型引起的碎片化结果及其成因。同时，本文提出基于通勤大数据的改进模型并设计求解算法。测试结果表明，改进的出行空间分布模型能够更充分地利用大数据的优势从而有效提高其对现实数据的重现能力。

测评的主要基础数据来自《2021年度中国主要城市通勤监测报告》^[9]收集的厦门市通勤OD数据，根据2020年9—11月百度地图位置服务和移动通信运营商手机信令数据推演得到城市人口居住地、就业地信息。移动通信运营商手机信令数据的有效时间间隔一般在2h之内^[10]，而人们一天中大多数时间会在家和就业地度过。基于较长时间周期的数据和适当的聚类算法，可从手机信令数据较为精确地推演用户的居住地和就业地^[8]。百度地图位置服务更多地融合了定位、导航和画像数据，与移动通信运营商手机信令数据相结合提供了城市人口翔实而客观的通勤OD数据。

厦门市域划分为37 926个分析单元，每个分析单元为250 m×250 m的栅格。在14.38亿个OD对上的每日通勤OD总量达到190.72万人次。测评的流程为：利用实际通勤OD(实际值)和交通网络数据标定双约束重力模型阻尼函数的参数，计算每个分析单元的通勤产生量和吸引量，再采用双约束重力模型计算通勤OD(计算值)，比对计算值与实际值的差异。

表1给出不同样本规模标定的出行空间分布模型在不同空间尺度上的模拟误差，其中阻尼函数变量u_pq为实际路网距离。全样本为采用所有样本进行标定。1/2样本和1/4样本是在每一个500 m×500 m的栅格中，分别抽取下面的两个250 m×250 m栅格和左下的一个250 m×250 m栅格，由这些栅格间的出行所构成的样本进行标定。这样保证样本在空间上分布的均匀性。1/8，1/16和1/32则是采用随机抽样从全样本中抽取，不能保证样本在空间上的均匀性。以和分别表示实际值和计算值，则出行空间分布模型的模拟误差为。显然，模拟误差最小为0，最大为100%。根据空间相关关系，可将边长250 m栅格的分析单元聚合到500 m栅格。从表1可以看出，当样本量足够大时，样本量的进一步增加并不会带来模型模拟精度的提升。也就是说，在传统空间分布模型框架下并不能充分发挥大数据的数量优势。在250 m栅格的分析单元上统计，传统出行空间分布模型的模拟误差接近70%。但即使在500 m栅格上，传统空间分布模型的模拟误差仍超过50%。

表2为全样本标定的模型计算值与实际值的对比情况。实际值显示巨量分析单元的真实通勤矩阵是一个非常稀疏的矩阵，存在通勤出行的OD对仅占OD对总数的0.078%，显而易见所有通勤量为正整数。而通过双约束重力模型计算的通勤OD矩阵，在所有O点产生量和D点吸引量大于0的OD对间均有大于0的计算值，0值OD对数占OD对总量的比例仅为38.54%。也就是说，大部分OD对间均有大于0的计算值，不小于1的OD对仅占OD对总量0.017%。计算值位于10^-5~10^-4的OD对数占OD对总量的比例高达20.464%。计算值小于1的通勤总数占总通勤量的比例达到63.95%。由此可见，计算的OD矩阵呈现为一个支离破碎的矩阵，本文称之为碎片化现象。

当前包括重力模型的所有主要出行空间分布模型都可以看作为目的地选择模型，个体选择一个目的地的概率会随着某种阻尼增加而下降。由于没有考虑个体的差异和目的地的异质，出行空间分布模型所描述的出行空间分布规律可以看成群体在统计上所表现的特征。对于个体而言，出行更多地表现为随机性。当把出行空间分布模型应用于分析单元时，分析单元所包含的个体越多，与统计上的规律越接近，而分析单元所包含的个体越少，则随机性更强，与统计特征的差异就越大。因此，随着近年来分析单元越来越小的趋势，采用当前出行空间分布模型预测的误差也就越大。

对于通勤出行总体而言，任意两地间的通勤量g_pq与阻尼函数成正比，这也就是传统重力模型，即g_pq∝f(u_pq)。

而针对具体的地点p，q，其通勤量g_pq与两地间通勤量的观测值正相关，因为通勤出行一旦生成就具有很强的延续性，人们不会每天早上去权衡各地的出行成本来重新选择上班的地点。实际数据表明，通勤者在一段时间内改变其居住地、工作地的比例非常低。因此，提出

式中：参数指在一个时间周期(比如一年)中通勤OD发生变化的概率(也可理解为在一个时间周期内人们对于以往出行遗忘的概率)；φ指观测值发生的时间距离预测时间的周期数；常数ω指两地间发生联系的基准概率或平均概率。上式表明，时间周期越短，通勤OD发生改变的概率越小。如果将一个分析单元的所有通勤者看成一个抽象的出行者，上式也可以采用记忆性随机游走模型的理论^[11]进行解释：个体在出行过程中对已经访问过的地点形成记忆性偏好，总是倾向于返回之前访问过的地点，这种记忆性偏好会随着个体对一个地点的访问次数增加而不断强化，也会随着时间的久远而减弱。

综合考虑出行总体的统计特征和个体的差异性，提出两地间新的通勤量公式，即

当f(u_pq)为常数且时，即通勤者对阻尼完全不敏感，而且对以往访问地没有记忆性偏好，上式即退化为随机分布模型；当f(u_pq)为常数，ω=0且时，即通勤者对阻尼完全不敏感而且对以往访问地存在一定程度的记忆性偏好，上式就会退化为传统增长率模型。传统增长率模型在应用时如果两个交通小区间出行量的观测性为零，那么未来年预测量也一定也为零。这极大地限制了增长率模型的应用范围。显然，当上式中f(u_pq)为常数，ω>0且时，上式就成为一个改进的增长率模型，克服了传统增长率模型使用范围的局限性。当f(u_pq)不为常数，且(或而φ→∞)，即通勤者对阻尼敏感，而且对以往访问地没有记忆性偏好(或者说出行没有延续性)，上式则退化为重力模型。

因此，新模型的构建如下：

式中：α_p和β_q为参数。式(2)~(4)分别为产生量、吸引量和总量约束，式(5)为非负约束。

上面提出的新模型可以采用经典的二维矩阵平衡算法进行求解。

首先计算，再运行二维矩阵平衡算法。

初始化：循环次数l=0，，∀p，，∀q.

步骤1(行平衡)：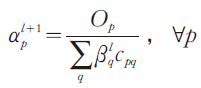

步骤2(列平衡)：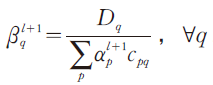

步骤3(收敛条件判断)：如果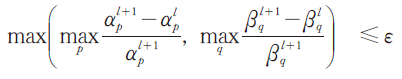或l=l_max，循环结束，得到结果矩阵；否则，令l=l+1，返回步骤1。

为了对比不同模型和参数变化对于现状通勤空间分布的重现能力，令φ=1，即取最小的时间周期数。ω=1，相当于传统出行空间分布模型的情形。由表3可以看出，提出的新模型在各种情况下均不逊于传统空间分布模型。在一定的基准概率下，越小(即变化的概率越小)，模拟误差越小，250 m栅格的模拟误差均高于500 m栅格。也就是说，出行的稳定性越高，惯性越大，重现时模拟误差越小(即可预测性更好)。基准概率ω最大可取中最小的正数(在本例中为1)，最小可取OD对上的平均出行量(即的总和除以总的OD对数，在本例中为0.001 3)。基准概率ω的相对大小反映了出行空间分布的灵活性。ω越大表示出行在空间上分布的灵活性越高，反之亦反之。显然，基准概率ω取小值对现状数据的重现会有较小的模拟误差。

当改进模型用于中长期预测时，时间周期数φ的取值越大，计算值相对于基准概率ω值就越小。这意味着计算值在OD对间的差异性变小了，f(u_pq)值的作用将更进一步凸显，因此改进模型的表现将向传统出行空间分布模型靠拢。而当城市处于较为稳定的发展阶段时，由于参数值较小，可以预期改进模型用于中长期预测的表现也会在一定程度上优于传统空间分布模型。

传统出行空间分布模型的模拟精度对标定模型的样本量并不敏感，其在不同空间尺度上对实际通勤分布的重现能力均表现出较大误差。源于结果的碎片化现象，当空间分析单元越小时，模型的模拟误差将相应增大。改进模型同时考虑出行总体的统计特征和个体的差异性，可以在一定程度上降低模拟误差。在传统预测框架下，以大数据代替小数据会极大地限制大数据的内在价值。随着交通领域大数据的日益丰富，基于大数据的预测模型架构创新将会是未来模型创新的主要方向。

封面图片来源：

《城市交通》自选图库

拍摄：江永

点击“阅读原文”查看

“观点集萃”栏目更多内容