 随着信息通信技术和物联网技术的迅猛发展,地理学家们越来越关注基于空间社会流数据的空间交互建模。在这一领域,核心研究议题之一是如何从大量的起点-终点(OD)流数据中提取区际流动模式,以揭示不同空间连续的区域群组间的相互关联。本研究针对这一议题,创新性地提出了一种新型的流时空聚类方法,旨在深入理解区域间的交互作用和区域协同流动模式。
然而,基于绝对交互流量的区际联系紧密关系测度忽略了区际相对联系紧密度在揭示区域协同模式方面的重要性。此外,OD流的时间维度与空间维度相分离甚至被忽略。为此,本研究首次引入了相对交互强度的概念及其量化方法,使得研究能够超越传统的仅基于交互量的流密度分析,考虑到源地和目的地间交互关系的相对紧密度及其时空扩展。与现有方法相比,本研究所提出的基于强度的聚类和评估方法能够从局部视角而非全局视角更准确地捕捉区域间相对联系的时空流动模式,展示了在识别和分析空间交互特征方面的显著优势。
通过对合成数据集的实验验证,证明了所提方法在流模式识别的有效性、高效性和精确度方面的显著优势。此外,通过对中国人口迁移数据的实际案例分析,本研究展示了该方法在揭示区域间隐含的时空关联模式方面的强大应用潜力。此方法不仅为地理信息科学、人文地理和城乡规划等领域提供了新的分析工具,也为复杂空间流建模和区域协同分析的相关研究开辟了新的前景。
随着信息通信技术和物联网技术的迅猛发展,地理学家们越来越关注基于空间社会流数据的空间交互建模。在这一领域,核心研究议题之一是如何从大量的起点-终点(OD)流数据中提取区际流动模式,以揭示不同空间连续的区域群组间的相互关联。本研究针对这一议题,创新性地提出了一种新型的流时空聚类方法,旨在深入理解区域间的交互作用和区域协同流动模式。
然而,基于绝对交互流量的区际联系紧密关系测度忽略了区际相对联系紧密度在揭示区域协同模式方面的重要性。此外,OD流的时间维度与空间维度相分离甚至被忽略。为此,本研究首次引入了相对交互强度的概念及其量化方法,使得研究能够超越传统的仅基于交互量的流密度分析,考虑到源地和目的地间交互关系的相对紧密度及其时空扩展。与现有方法相比,本研究所提出的基于强度的聚类和评估方法能够从局部视角而非全局视角更准确地捕捉区域间相对联系的时空流动模式,展示了在识别和分析空间交互特征方面的显著优势。
通过对合成数据集的实验验证,证明了所提方法在流模式识别的有效性、高效性和精确度方面的显著优势。此外,通过对中国人口迁移数据的实际案例分析,本研究展示了该方法在揭示区域间隐含的时空关联模式方面的强大应用潜力。此方法不仅为地理信息科学、人文地理和城乡规划等领域提供了新的分析工具,也为复杂空间流建模和区域协同分析的相关研究开辟了新的前景。

引用格式:Haiping Zhang, Xingxing Zhou*, Xinyue Ye, Guoan Tang, Haoran Wang & Shangjing Jiang (2023) Strength-weighted flow cluster method considering spatiotemporal contiguity to reveal interregional association patterns, GIScience & Remote Sensing, 60:1, 2252923.
Link: https://doi.org/10.1080/15481603.2023.2252923
两个区域之间的联系紧密程度可以通过某种流动要素在单位时间(或指定时段)内的流动速率指标化反映,这些流动要素可以是人流、物流、信息流等。流动速率越高,则说明区域之间的联系越紧密,反之则越不紧密。这种仅通过具有某种交互关系的区域之间的流动要素的流动效率来反映的紧密程度可以称之为绝对联系紧密程度。因为它的值不受其他区域流动要素的直接影响。
然而,在多数情况下,人们更加关注区域之间的相对联系紧密程度。所谓相对联系紧密程度,是指某一区际之间的流动要素的流动效率同时对流出区域(源区域Origin)和流入区域(目标区域Destination)的重要程度。它的值受到源区域所有流出要素和目标区域所有流入要素的影响。
在本研究中,我们将区域之间的绝对联系紧密程度用交互密度(interaction density, ID)表述,而将相对联系紧密程度用交互强度(interaction strength, IS)表述。为了进一步明晰两者的内涵及其区别,下面给出一个例子。
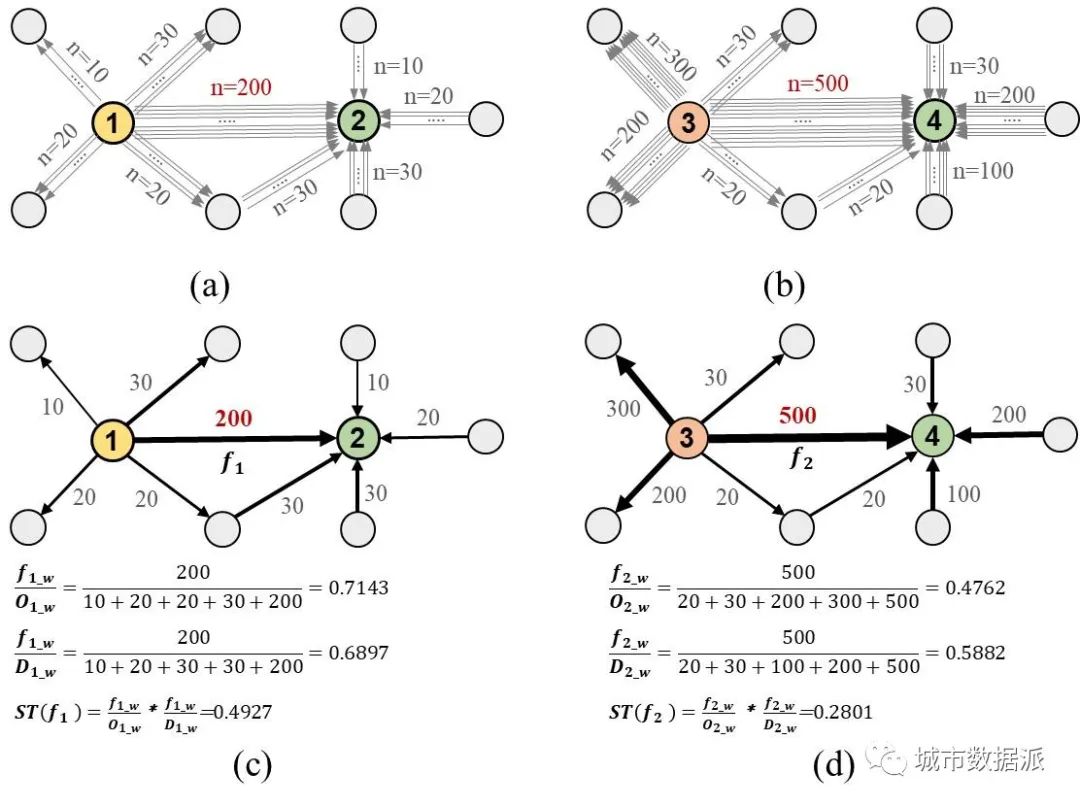
上文提到源区域和目标区域之间的流动效率(流密度)反映了它们之间联系的绝对紧密程度。例如,在图1(a)和(b)所示的流动中,区域1到2的流动单元数为200个,而区域3到4的流动单元数为500个,说明区域1的密度大于区域2,区域3和区域4之间的联系更紧密。但在图1(c)和(d)中,如果将源区域和目标区域之间的流量作为单个流动单元的权重,则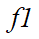 和
和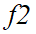 的交互强度(相对联系紧密程度)可分别被计算。在图1(c)中,加权流量
的交互强度(相对联系紧密程度)可分别被计算。在图1(c)中,加权流量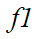 对源区域1的重要性远高于该源区域的其他流入流量(权重较大),其重要性占比为0.7143。它对目标区域2的重要性也远远大于其他流入流量,其重要性占比为 0.6897。同样,
对源区域1的重要性远高于该源区域的其他流入流量(权重较大),其重要性占比为0.7143。它对目标区域2的重要性也远远大于其他流入流量,其重要性占比为 0.6897。同样,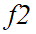 对于源区域3和目标区域4的重要性占比分别为0.4762和0.5882。最后,可以计算出
对于源区域3和目标区域4的重要性占比分别为0.4762和0.5882。最后,可以计算出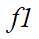 和
和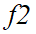 的强度分别为0.4926和0.2801,即
的强度分别为0.4926和0.2801,即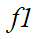 对区域1和2两者作为整体时的重要性比重为0.4926,
对区域1和2两者作为整体时的重要性比重为0.4926,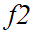 对区域3和4两者整体性的重要性比重为0.2801。即两个区域组(1和2, 3和4)的交互强度分别为0.4926和0.2801。
可以发现,虽然区域1到区域2的交互密度(绝对联系紧密程度)远大于区域3到区域4,但区域1到区域2的交互强度(相对联系紧密程度)大于区域3到区域4。这个示例让我们意识到,两个区域之间的交互,从相对联系紧密程度和绝对紧密程度来看,可能存在截然相反的关系。但需要意识到它们具有截然不同的内涵。
对区域3和4两者整体性的重要性比重为0.2801。即两个区域组(1和2, 3和4)的交互强度分别为0.4926和0.2801。
可以发现,虽然区域1到区域2的交互密度(绝对联系紧密程度)远大于区域3到区域4,但区域1到区域2的交互强度(相对联系紧密程度)大于区域3到区域4。这个示例让我们意识到,两个区域之间的交互,从相对联系紧密程度和绝对紧密程度来看,可能存在截然相反的关系。但需要意识到它们具有截然不同的内涵。
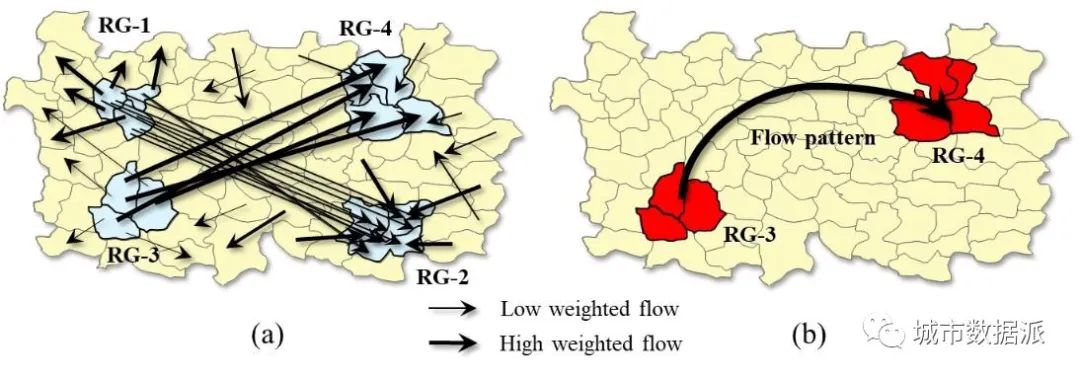
本文旨在解决两个问题,两个问题之间的关系为:解决第一个问题是解决第二个问题的前提。现有的区域间关联模式通过OD流量密度揭示了源区与目的区之间的绝对紧密性,但未能捕捉到源区与目的区之间可能存在的:尽管在全局上绝对联系紧密性相对较低但却具有较强相对联系紧密的局部关联模式。
(1) 如何从一组交互强度加权OD流中识别出相对联系紧密程度较高的区际协同模式?
如图2所示,为了具体阐释问题1,将每个区域组编号为RG-1至RG-4。在图2(a)中,RG-1和RG-2之间存在许多低权重的流单元。但由于RG-1流向其他区域的流单元较多,因此RG-1流向RG-2的流量所占从RG-1流出的所有流量的比例较小。由于更多来自其他区域的高权重流单元流入目标区域RG-2,因此RG-1流向RG-2的流量占流入到RG-2的总流量的比例较小。这导致从RG-1到RG-2的流量对于RG-1和RG-2的重要性较低,即两个区域之间的交互强度很小。
相反,RG-3和RG-4之间的流单元大多具有较大的流动强度,且这些流动单元彼此相邻,导致RG-3和RG-4之间的交互强度较大。这形成了一种区域群组之间的协同关联模式,如图2(b)所示。即构成RG-3的各个区域单元的大多数流动要素都流向了构成RG-4的各区域单元。同时,构成RG-4的各流动单元中流入的流动要素,大多来自于RG-3。本文的目标之一是通过算法识别出这种具有相对联系紧密程度的区域组间协同关联模式。需要注意的是,所谓空间连续,是指每个区域组中的空间单元是空间邻近的。如构成RG-1的各个空间区域单元在空间上是连续的。
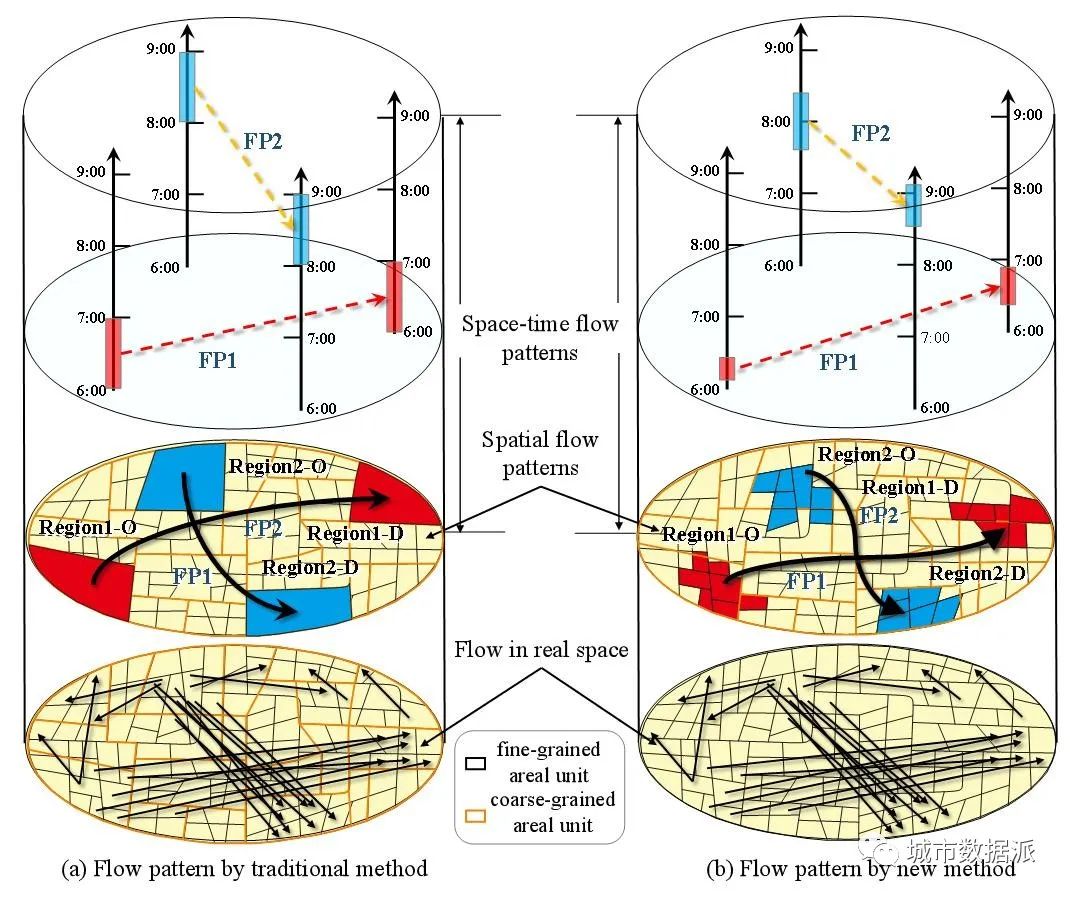
时空OD流不仅包含空间位置信息,还包含时间维度信息。空间和时间是不可分割的,应该被视为一个整体。从时空流中提取的区域间关联模式还应具有时空属性,即不仅要获得区域间关联模式中包含的流单元集合——源区域和目标区域的集合,还要获得流模式的源、目标区域集中OD流的持续时间。实现这一目标是本研究的第二个需要解决的问题。
(2) 如何通过将流单元的时空维度视为一个整体来捕捉具有任意空间聚集形状和任意持续时长的区域群组间的协同关联模式?
为了进一步阐明上面的问题2,图3提供了一个具体的解释。我们首先撇开从大量OD流量数据中挖掘区域间关联模式的复杂性及其挑战。相反,我们使用一个简单的例子来说明考虑流动单元的空间和时间接近性的重要性和复杂性,以及现有简单粗暴处理方式的严重缺点。
图3中的例子具体暴露了通过预定义的空间区域和时间窗口挖掘的时空流模式中的问题。图3(b)中的Layer 1与图3(a)中的Layer 1相同,包含同一组划分为许多子区域的流单元。在现实世界的真实案例中,区际协同模式FP1和FP2的空间范围可能类似于图3(b)中的第2层,时间周期可能类似于图3(b)中的第3层。显然,更加符合现实的流模式的起点或终点区域组可能比图3(a)中的小或大。持续时间也可能跨越当前预定义的每小时。总体来看,目前的方法由于未考虑时空连续性,导致难以兼顾空间区域上的真实形状和时间上的真实时长,难以达到如图3(b)所示的效果。
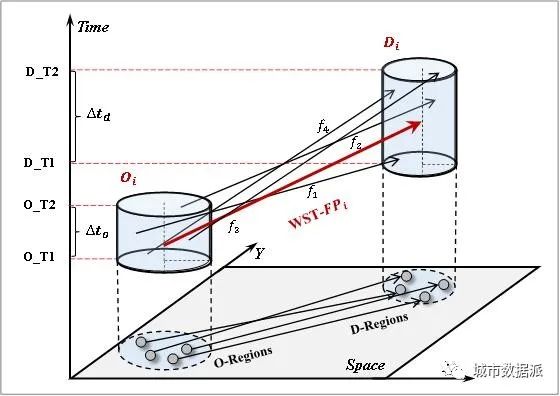
本研究尝试提出一种时空连续的区际流模式聚类方法,在不预先定义区域或时间段的情况下,快速准确地检测任意形状OD区域之间的任意时段存在的强度加权的时空流模式(WST-FP)。
这里简要介绍了从大规模OD流单元中挖掘所有WST-FPs的过程。如图4(a)所示,首先在所有流单元中选取强度最大的流动单元
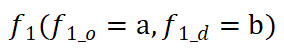 作为种子流单元,并将其标记为已访问。然后,找到流动单元
作为种子流单元,并将其标记为已访问。然后,找到流动单元
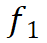 的原点
的原点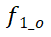 和终点
和终点
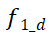 的所有相邻区域元素;如图4(b)所示,c是源区域
的所有相邻区域元素;如图4(b)所示,c是源区域
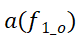 的其中一个邻接区域元素,d是目标节点
的其中一个邻接区域元素,d是目标节点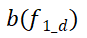
 的其中一个邻接区域元素。我们注意到
的其中一个邻接区域元素。我们注意到
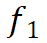 的起始点和终点的几个相邻区域之间没有流单元。因此,应从相邻集合中剔除此类区域元素,得到由起点
的起始点和终点的几个相邻区域之间没有流单元。因此,应从相邻集合中剔除此类区域元素,得到由起点
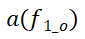 和终点
和终点
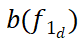 的相邻区域元素组成的流单元集合。
的相邻区域元素组成的流单元集合。
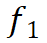 和图4(c)中的其他流动单元满足本文定义(见原文)的空间距离可达条件。
然后,对上述流单元集合中的每个流进行类似的过滤,只保留到
和图4(c)中的其他流动单元满足本文定义(见原文)的空间距离可达条件。
然后,对上述流单元集合中的每个流进行类似的过滤,只保留到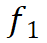
 的时间距离满足阈值τ的流单元,称为
的时间距离满足阈值τ的流单元,称为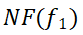
 ,如图4(d)所示。
随后,将流动单元
,如图4(d)所示。
随后,将流动单元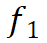
 与其他与
与其他与
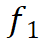 具有时空邻近关系的流单元进行组合,并确定每个组合的流动强度可达性,如图4(e)所示。如果将新WST-FP的流单元集标记为FP,则将
具有时空邻近关系的流单元进行组合,并确定每个组合的流动强度可达性,如图4(e)所示。如果将新WST-FP的流单元集标记为FP,则将
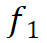 和所有其他满足可达时空距离和流强度的流单元
和所有其他满足可达时空距离和流强度的流单元 作为该模式的流单元
作为该模式的流单元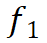 成员放置在集合FP中。
成员放置在集合FP中。
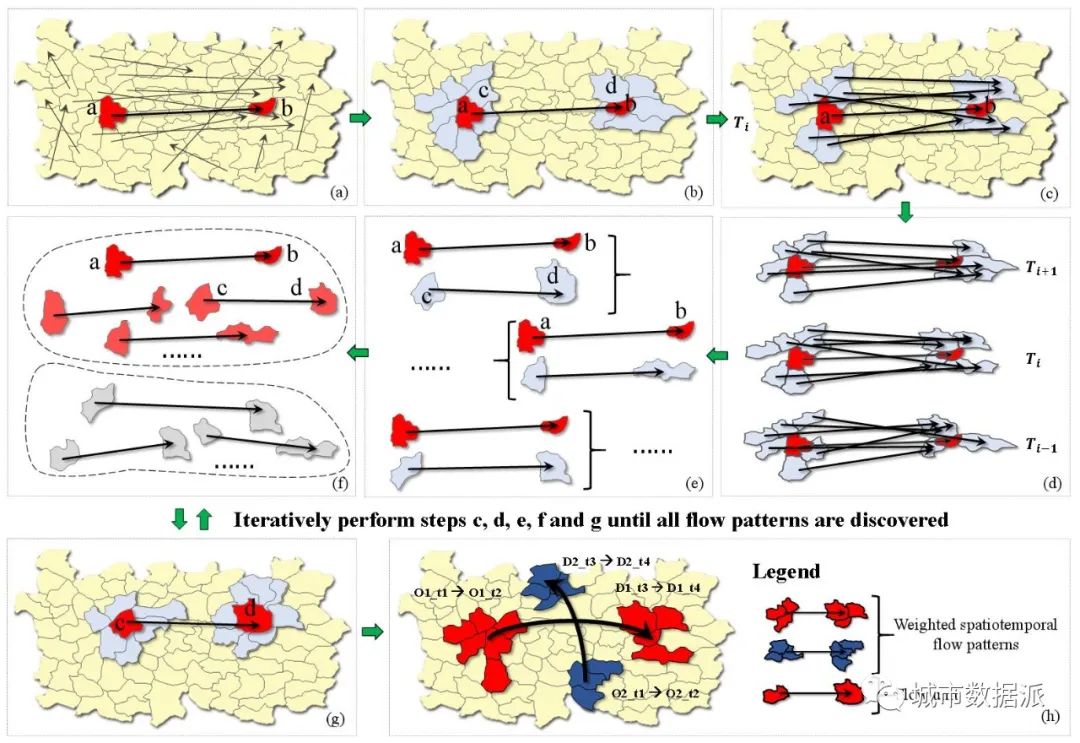
最后,选择满足时空接近和强度可达的任何流单元作为下一个种子流单元,并标记为已访问,重复图4(b)至(e)所示的过程。这里以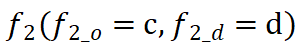
 为种子流单元,标记为已访问。进入图4(f)中,并返回到类似于图4(b)中的流程。迭代继续,直到集合WST-FP中的每个流单元被标记为访问。最终,FP中的流单元共同构成一个新的WST-FP,如图4(h)所示,这是WST-FP的示意图
一个完整的 WST-FP 包含至少两个流单元,并且流动模式的源区域或目标区域由至少两个了邻近区域组成。WST-FP 包含许多基本属性变量,这些变量对于测量模式和计算各种特征至关重要。WST-FP 可以表示为
为种子流单元,标记为已访问。进入图4(f)中,并返回到类似于图4(b)中的流程。迭代继续,直到集合WST-FP中的每个流单元被标记为访问。最终,FP中的流单元共同构成一个新的WST-FP,如图4(h)所示,这是WST-FP的示意图
一个完整的 WST-FP 包含至少两个流单元,并且流动模式的源区域或目标区域由至少两个了邻近区域组成。WST-FP 包含许多基本属性变量,这些变量对于测量模式和计算各种特征至关重要。WST-FP 可以表示为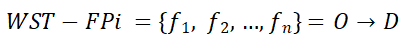 ,n表示 WST-FP 中的流单元数量,O 和 D 分别表示源区域组和目标区域组的时空属性。 然后,对于任何流单元
,n表示 WST-FP 中的流单元数量,O 和 D 分别表示源区域组和目标区域组的时空属性。 然后,对于任何流单元
 ,至少有一个流单元满足时空邻近性和阈值条件
,至少有一个流单元满足时空邻近性和阈值条件 。
在空间级别上,
。
在空间级别上, 的起始区域集可以表示为
的起始区域集可以表示为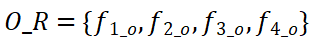 ,目标区域集可以表示为
,目标区域集可以表示为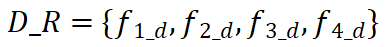
 。然后,共同构成
。然后,共同构成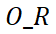 和
和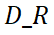
 共同构成WST-FPi基本空间特征量。
在时间层面上,每个流量单元的起始区域对应一个起始时刻
共同构成WST-FPi基本空间特征量。
在时间层面上,每个流量单元的起始区域对应一个起始时刻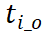
 ,每个 流量单元的目标区域对应一个到达时刻
,每个 流量单元的目标区域对应一个到达时刻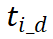
 。WST-FPi的起始区域的时间段可以表示为
。WST-FPi的起始区域的时间段可以表示为
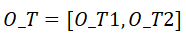 ,这里的
,这里的
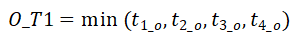 表示起始区域所有起始时刻中存在的最早起始时刻,表示最晚起
表示起始区域所有起始时刻中存在的最早起始时刻,表示最晚起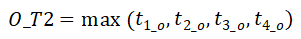 始时刻。同时,目的区域的时间段可以表示为
始时刻。同时,目的区域的时间段可以表示为
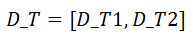 ,其中
,其中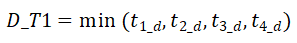
 表示目标区域所有到达时刻中最早到达的时刻,
表示目标区域所有到达时刻中最早到达的时刻,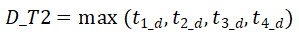 表示最晚到达的时刻。WST-FPi 的起始区域的持续时间为
表示最晚到达的时刻。WST-FPi 的起始区域的持续时间为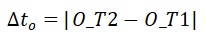 ,其目标区域的持续时间为
,其目标区域的持续时间为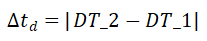 。 整个WST-FPi的持续时间为
。 整个WST-FPi的持续时间为
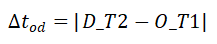 。
。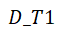
 ,and
,and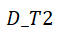 and
and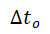
 ,
,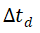
 ,
,  and
and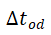 共同构成了WST-FPi的基本时间特征量(图5)。
共同构成了WST-FPi的基本时间特征量(图5)。

区域间OD流动模式的覆盖率、接近度和复合度的指标最初是由Kim等人提出的。用于评估流动密度的聚类结果(Kim等人,2014)。后来,它被 Zhang 等人应用于强度加权流聚类结果的评估(Zhang, et al. 2018)。本文进一步对其进行了细化和扩展,使其适用于时空强度加权流型聚类结果的评估。
覆盖率是指在计算分析中,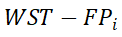 中相互作用体积之和与相同开始时间段或到达时间段的所有流单元的相互作用体积之和之比,用于反映整个流数据中目标流模式
中相互作用体积之和与相同开始时间段或到达时间段的所有流单元的相互作用体积之和之比,用于反映整个流数据中目标流模式
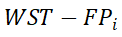 的重要性程度。在指定的时间段内
的重要性程度。在指定的时间段内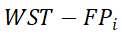
 的覆盖率公式可以表示为:
的覆盖率公式可以表示为:
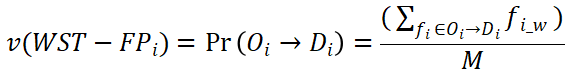
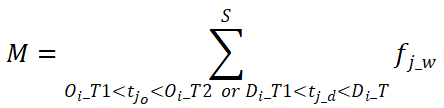
其中 是在时段
是在时段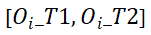 内从源区域
内从源区域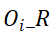 到
到
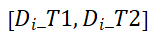 时段内的目标区域
时段内的目标区域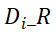 的概率。该流单元集合的开始时间在时段
的概率。该流单元集合的开始时间在时段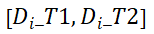 或时段
或时段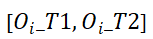 内。
内。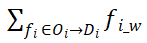 表示
表示
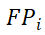 中的总交互流强度和.
中的总交互流强度和.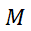 表示在时段
表示在时段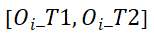 或时段
或时段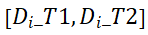 内的总交互流强度和.
任何一个
内的总交互流强度和.
任何一个
 的源区域集合都是
的源区域集合都是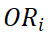
 ,从
,从
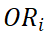 流出的总流用
流出的总流用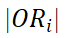 表示。目的区域的集合是
表示。目的区域的集合是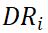
 ,到达目的区域的总流量用
,到达目的区域的总流量用 表示。对于任意一个
表示。对于任意一个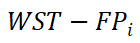
 , s值用来表示这个流模式的交互紧密程度。此外,利用s值反映流型中起点和终点区域之间的相关性强弱。计算公式为:
, s值用来表示这个流模式的交互紧密程度。此外,利用s值反映流型中起点和终点区域之间的相关性强弱。计算公式为:
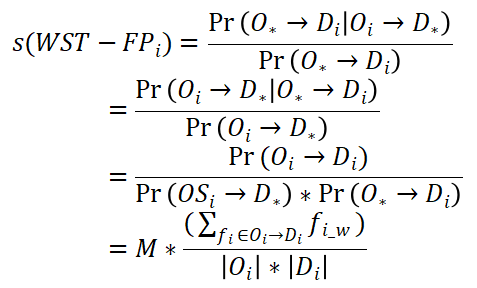

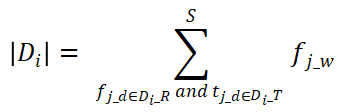
式中
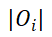 表示起源区域为
表示起源区域为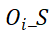
 、起始时间为
、起始时间为
 时段的流单元相互作用总量。
时段的流单元相互作用总量。
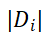 表示目的区域为
表示目的区域为
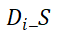 在时间段
在时间段
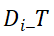 内到达时间的流单元的相互作用总量。
内到达时间的流单元的相互作用总量。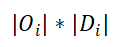
 表示从源区域到目的区域的总流量与总流量的乘积。
表示从源区域到目的区域的总流量与总流量的乘积。
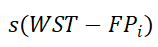 值越大,该流型的始发区与目的区之间的相关性越强。
值越大,该流型的始发区与目的区之间的相关性越强。
覆盖率从流本身反映模式的范围,紧密度通过流模式的起源
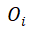 和目的
和目的
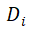 之间的相关性反映模式的强度。这两个指标从局部角度评价了WST-FP的强度,具有一定的局限性。本文采用覆盖率和准确率的综合值来综合反映模式的强度。具体公式为:
之间的相关性反映模式的强度。这两个指标从局部角度评价了WST-FP的强度,具有一定的局限性。本文采用覆盖率和准确率的综合值来综合反映模式的强度。具体公式为:
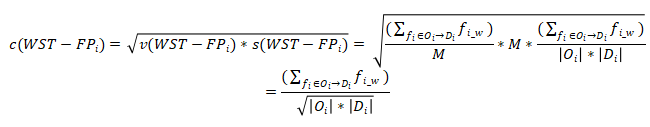
为了验证本文提出的WST-FPs挖掘方法的有效性,设计了两个合成数据集。其中一个是简单数据集,另一个是复杂数据集。图 9为一组加权时空 OD流量单位,图 9(a)显示了所有OD流的时空分布,而研究区和基本区及其编号代码如图 9(c)所示。
如果这里以共享的边或顶点作为空间邻近规则,以半小时为时间间隔,从图9(b)中可以看出,{f1, f2, f3, f4}是一个流模式,记为WST-FP1。{f5, f6, f7}为检测到另一种流模式,记为WST-FP2。在图9(b)中,f8在空间上与WST-FP1中的流动单元相邻,但在时间上不相邻。F9在空间和时间上都不与任何模式相邻。因此,WST-FP1和WST-FP2中都不包含f8和f9。虽然其他OD流单元在空间和时间上满足邻近规则,但其中一些相互作用体积可能对型线所在区域的贡献较小。此时,这些OD流量单元也不能被视为模式的一部分。最后,我们期望得到如图9(d)所示的区域协同流模式结果,对应的评估指标如表2所示。

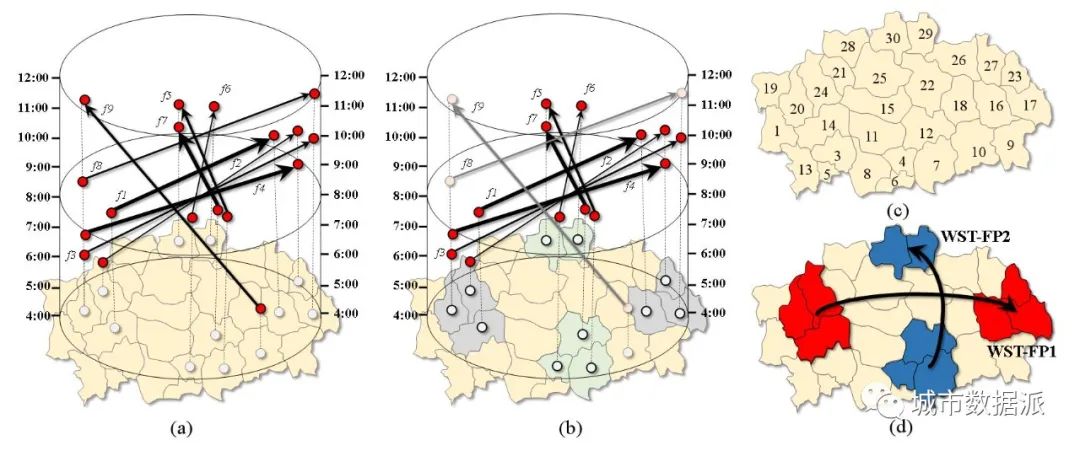
表 2. 基于小规模合成数据集的流模式指标(时间段单位:分钟)

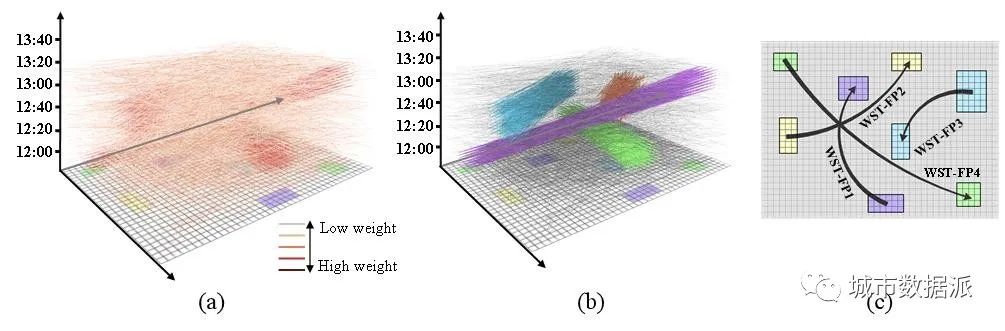
为了进一步验证本文提出的算法,我们设计了一个40行30列,时间段为12:00 – 13:40的时空格网。生成一个包含随机交互量值的大规模OD流单元集合,如图10(a)所示。该数据集还包含一些标记的OD流单元,它们构成了预设的流模式,如图10(b)所示。该算法用于从该数据集中发现时空流模式。合并阈值设置为0.0009,时间步长设置为10分钟。最后给出了分析结果,如图10(c)所示,对应的评估指标如表3所示。

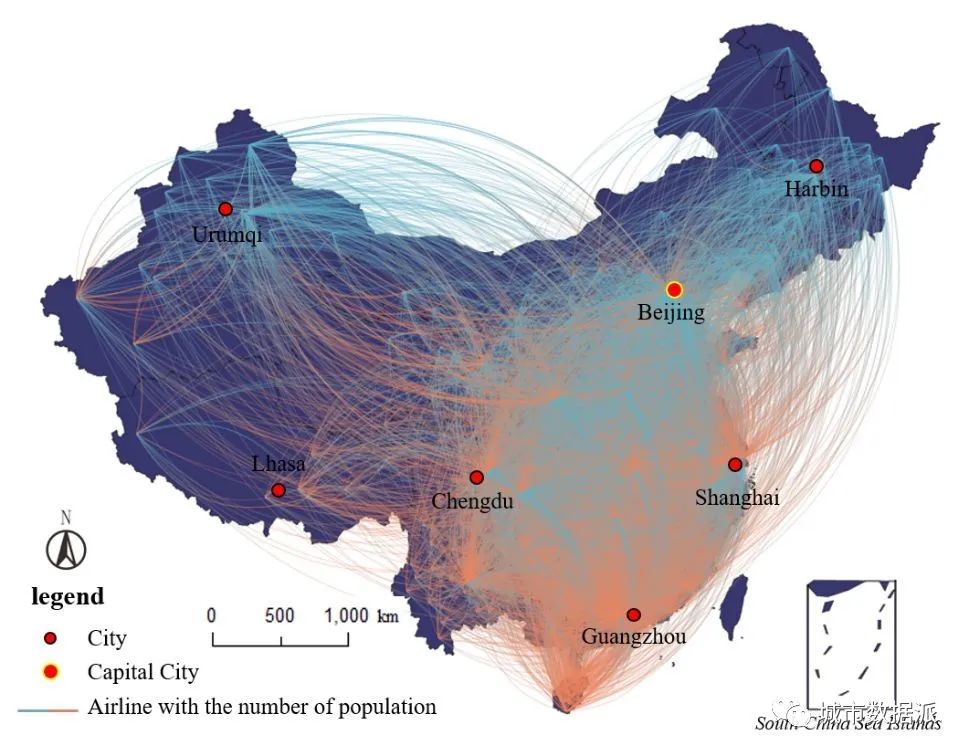
本研究选取中国大陆作为研究区域,如图13所示。大约有300个地级市,它们是第三级行政区域。使用的数据是中国境内每天乘坐飞机出行的人流数据。流动数据以三级行政区划的地级市为基本空间单元进行统计。数据来源于腾讯位置大数据开放平台。使用2018年全年的每日人流数据,即图13中OD线所示的流量单元数据是2018年某一天所有统计数据的可视化结果,获得2018年全年约250万条OD流数据。每条记录包含流单元的发生日期、起源、目标和交互量。地级市为来源地和来源地单位。中国航空管理局公司的统计数据显示,2018年我国航空客流量总额为6.1亿人次,其中包括出境和入境游客。即数据占总数的27.87%。图13引用自Zhang et al. (Zhang, et al. 2018),并使用与Zhang论文相同的数据集来验证本文的算法。
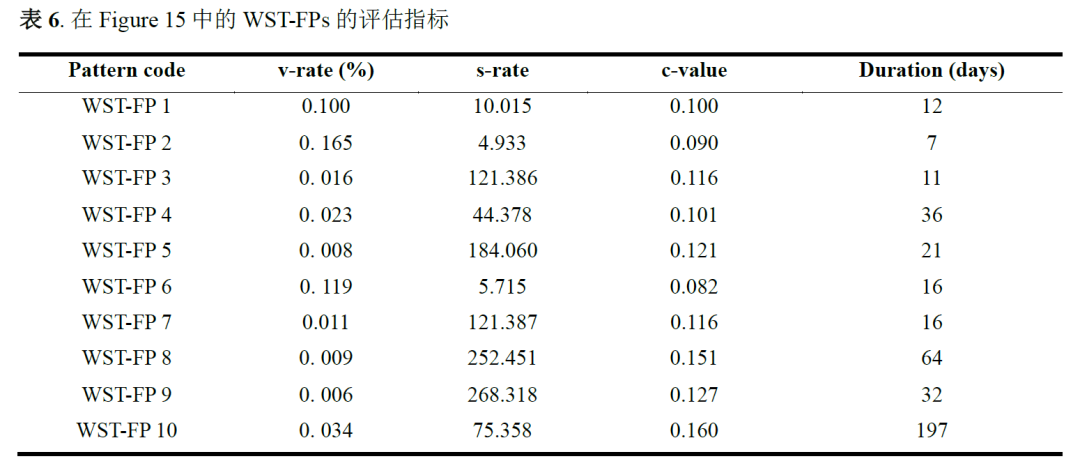
在真实数据集上,利用拓扑邻近规则对区域之间的空间关系进行建模。当两个区域有共同的边或顶点时,它们被标记为空间邻近。在这种情况下,将持续时间阈值设置为2天,即流发生在比当前时间早或晚2天的时间。合并阈值设置为0.009。在阈值约束下发现了大约50种流模式,其中21种模式在地图上可视化,如图14和15所示。在这里,为了进行对比分析,起点和终点区域之间距离较近的流模式放置在图14中,距离较远的放置在图15中,对应的评估指标结果分别如表5和表6所示。
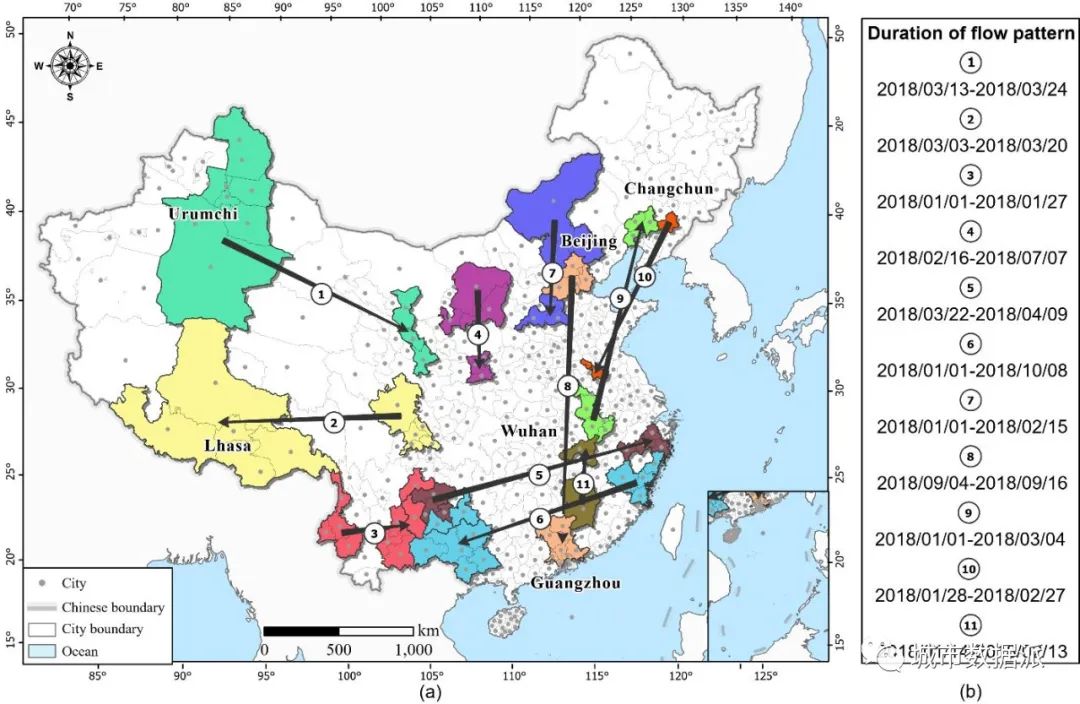
图14 中短距离为主的强度加权的时空区域协同流模式可视化结果
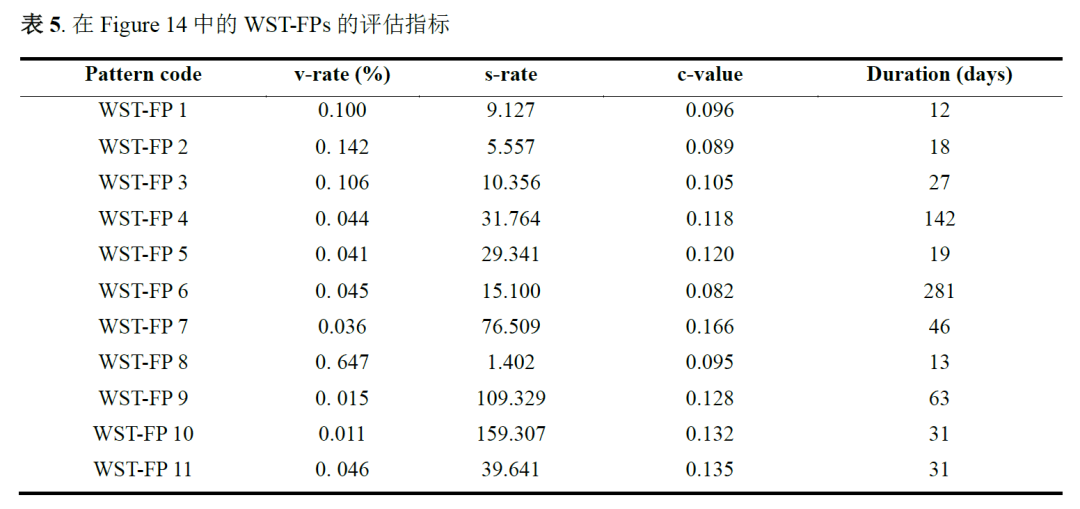
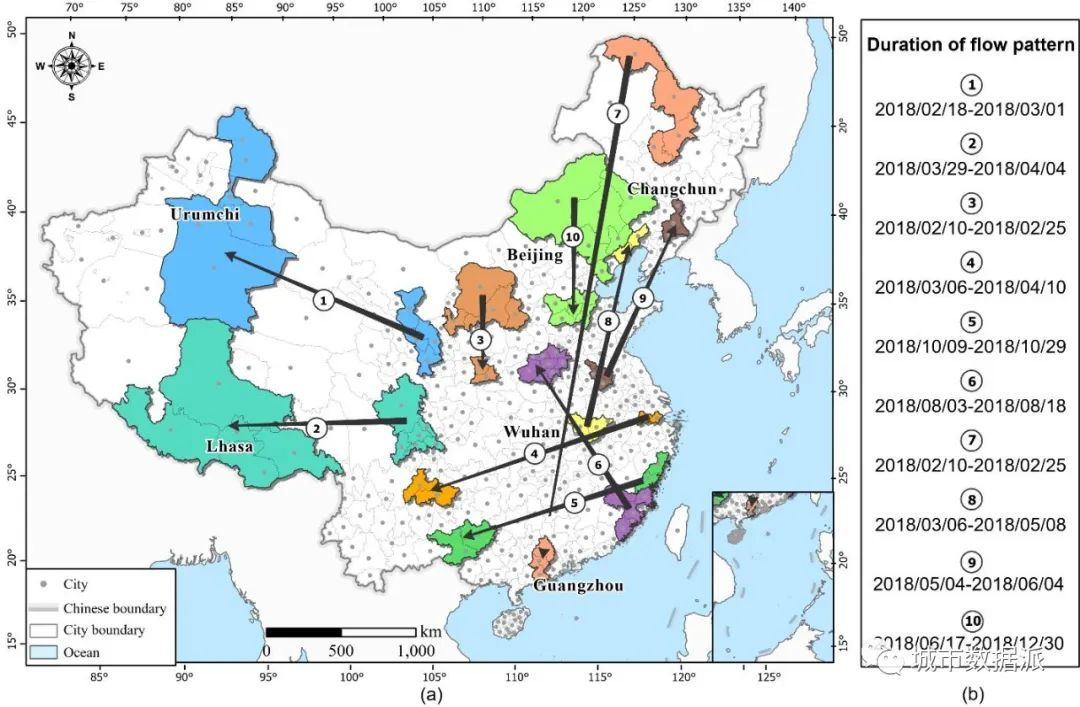
图15 中长距离为主的强度加权的时空区域协同流模式可视化结果
在理解区域间流量密度与流量强度之间的差异时,了解流量强度在解决实际问题中的关键作用以及它与流量密度的不同之处非常重要。为了阐明这一点,这里有一个示例。假设有三个区域:A区、B区和C区,如图17(a)所示。图17(b)可以看作是现实世界供需关系的空间网络抽象。C区为A区和B区提供许多重要资源。具体来说,C区向A区的资源流量为500(这个500可以近似为流量密度的值),而A区从其他所有区域的总资源流量仅为100。相比之下,虽然C区向B区的资源流量也高达600,但B区从其他区域的总资源流量远高,达到5000。如果发生灾难导致C区与外界隔离,这将严重影响A区的生产和生活。例如,如果C区发生事故无法向其他区域供应资源,对B区的影响相对较小,因为它从C区接收的资源仅占其总量的10.7%。然而,同样的事故对A区的影响将是巨大的,因为它从C区接收的资源占其总量的83.3%。这突出了流量强度如何反映特定互动对一个区域的重要性和依赖性,这与仅仅流量密度的大小不同。准确掌握流量强度对于分析区域网络和应对突发事件至关重要。
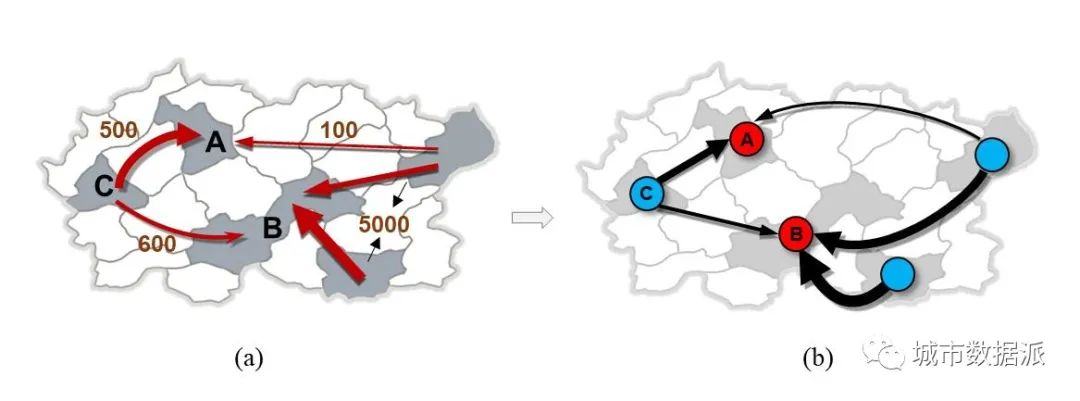
图17. 流动强度的实际应用举例。(a)现实世界的区域间供需链网络; (b)抽象后的区域间供应链网络。
传统基于未加权OD(起点-终点)流的聚类结果主要反映了密度特征,而本研究中基于加权OD流的聚类结果则捕捉到了区域间关联的强度。与现有方法中揭示区域间绝对接近度的流量密度不同,我们方法中的流量强度揭示了区域间的局部相对联系紧密程度。本研究引入了一种流量聚类算法,从传统的未加权聚类到加权聚类,从空间聚类到时空聚类,为综合时空流量模式挖掘提出了新的方法。此外,这种方法可以被视为空间OD流数据的一种新型地图概括技术。该方法的主要目标是解决诸如识别互动或关联强烈的区域、确定具有显著关联的流量模式中起源地和目的地的边界、以及理解这些关联何时发生等问题。这种方法在城市规划、交通分析和区域规划中具有重要潜力,这些领域涉及人流、物流、交通流和信息流等空间流元素的更广泛流空间视角。
基于强度的区域间局部相对接近性的概念,使我们能够揭示区域间连接的优先级和重要性。在资源有限的区域发展实际决策场景中,确定哪些区域间的连接最重要、应优先加强或保护变得至关重要。局部相对接近度便于比较不同区域及其邻近区域之间的接近度,从而识别最关键的区域关联,为决策者提供了明智选择的依据。例如,在城市交通规划中,确定新路线的方向需要了解哪些区域之间的联系最紧密。局部相对接近度可以识别这些区域,指导它们之间的连通性建立。同样,在疾病预防和控制中,确定隔离高风险区域的顺序需要考虑它们与感染区域的连接紧密程度。局部相对接近度可以指导优先隔离与感染区域连接最紧密的地区,有效遏制疾病的传播。
总之,与简单的绝对接近度测量相比,局部相对接近度为分析区域间关系提供了更准确、更现实的结果。在实践中,这种方法可以帮助规划者采取更科学、更有针对性的策略,例如在疾病控制中实施隔离措施或在城市规划中制定交通网络计划。
空间交互是一个常通过不同区域之间的关联来体现的概念。分析空间交互涉及考察互动事件的关键属性,如开始时间、结束时间、持续时间和互动强度。这些属性对于理解和研究空间交互模式至关重要。在考虑区域间的邻近性时,通常评估两个方面:全局绝对联系紧密程度和局部相对联系紧密程度。全局绝对联系紧密程度指的是区域间的直接连接,而不考虑区域与其邻近区域之间的关系,是绝对量。另一方面,局部相对联系紧密程度考虑的是区域之间的联系紧密程度相对于该源和目标区域与其他区域联系的紧密程度,是相对量。为了有效揭示区域交互规律,考虑OD流中的交互强度和时间至关重要。这些流作为聚类和分析OD数据的基本指标,使人们能够更准确地理解流量模式,并在该领域增强整体知识。通过结合这些指标,研究人员可以更深入地洞察区域间的空间交互动态。
本文提出了基于交互强度从大规模OD流中高效挖掘具有时空连续性的区域协同流模式的算法。它还引入了覆盖率、接近度和权衡等指标,作为评估流量模式有效性和准确性的手段。研究的主要焦点是解决根据交互强度加权的时空OD流对合并规则的挑战、合并过程中流量强度的计算,以及使用指标评估和解释流模式。
在测量绝对联系紧密程度时,常见的方法是考虑简单流量或区域间的互动次数。然而,在考虑局部相对联系紧密程度时,就需要考虑区域的邻域环境和互动范围。这需要采用更复杂的指标,如流量强度,来评估区域间的邻近性。所提出的算法以其效率为特点,在构建时空索引时时间复杂度小于O(n2)。如果包括交互流量和时间属性,还被设计为适用于各种类型的OD流数据。该算法参数化良好,仅需两个输入参数:时空邻近规则和强度可达性阈值。通过使用合成和真实数据集进行的案例实验,证明了该方法的稳健性和实用性。这些实验用于验证所提出算法在现实场景中的有效性和适用性。
最近有朋友问我们:为什么没有及时看到推文?因为微信改了推送规则,没有点“赞”或“在看”,没有把我们“星标”,都有可能出现这种状况。
加“星标”,不迷路!看完文章顺手点点“赞”或“在看”,就可以准时与我们见面了~
原文始发于微信公众号(城市数据派):GIScience & Remote Sensing | 强度加权的时空流聚类方法以揭示区际协同关联模式丨城市数据派





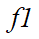 和
和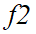 的交互强度(相对联系紧密程度)可分别被计算。在图1(c)中,加权流量
的交互强度(相对联系紧密程度)可分别被计算。在图1(c)中,加权流量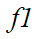 对源区域1的重要性远高于该源区域的其他流入流量(权重较大),其重要性占比为0.7143。它对目标区域2的重要性也远远大于其他流入流量,其重要性占比为 0.6897。同样,
对源区域1的重要性远高于该源区域的其他流入流量(权重较大),其重要性占比为0.7143。它对目标区域2的重要性也远远大于其他流入流量,其重要性占比为 0.6897。同样,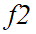 对于源区域3和目标区域4的重要性占比分别为0.4762和0.5882。最后,可以计算出
对于源区域3和目标区域4的重要性占比分别为0.4762和0.5882。最后,可以计算出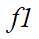 和
和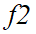 的强度分别为0.4926和0.2801,即
的强度分别为0.4926和0.2801,即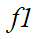 对区域1和2两者作为整体时的重要性比重为0.4926,
对区域1和2两者作为整体时的重要性比重为0.4926,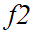 对区域3和4两者整体性的重要性比重为0.2801。即两个区域组(1和2, 3和4)的交互强度分别为0.4926和0.2801。
对区域3和4两者整体性的重要性比重为0.2801。即两个区域组(1和2, 3和4)的交互强度分别为0.4926和0.2801。







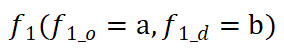 作为种子流单元,并将其标记为已访问。然后,找到流动单元
作为种子流单元,并将其标记为已访问。然后,找到流动单元
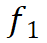 的原点
的原点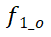 和终点
和终点
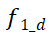 的所有相邻区域元素;如图4(b)所示,c是源区域
的所有相邻区域元素;如图4(b)所示,c是源区域
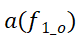 的其中一个邻接区域元素,d是目标节点
的其中一个邻接区域元素,d是目标节点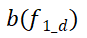
 的其中一个邻接区域元素。我们注意到
的其中一个邻接区域元素。我们注意到
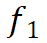 的起始点和终点的几个相邻区域之间没有流单元。因此,应从相邻集合中剔除此类区域元素,得到由起点
的起始点和终点的几个相邻区域之间没有流单元。因此,应从相邻集合中剔除此类区域元素,得到由起点
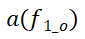 和终点
和终点
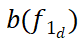 的相邻区域元素组成的流单元集合。
的相邻区域元素组成的流单元集合。
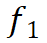 和图4(c)中的其他流动单元满足本文定义(见原文)的空间距离可达条件。
和图4(c)中的其他流动单元满足本文定义(见原文)的空间距离可达条件。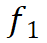
 的时间距离满足阈值τ的流单元,称为
的时间距离满足阈值τ的流单元,称为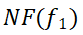
 ,如图4(d)所示。
,如图4(d)所示。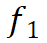
 与其他与
与其他与
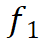 具有时空邻近关系的流单元进行组合,并确定每个组合的流动强度可达性,如图4(e)所示。如果将新WST-FP的流单元集标记为FP,则将
具有时空邻近关系的流单元进行组合,并确定每个组合的流动强度可达性,如图4(e)所示。如果将新WST-FP的流单元集标记为FP,则将
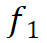 和所有其他满足可达时空距离和流强度的流单元
和所有其他满足可达时空距离和流强度的流单元 作为该模式的流单元
作为该模式的流单元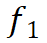 成员放置在集合FP中。
成员放置在集合FP中。

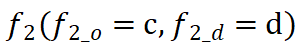
 为种子流单元,标记为已访问。进入图4(f)中,并返回到类似于图4(b)中的流程。迭代继续,直到集合WST-FP中的每个流单元被标记为访问。最终,FP中的流单元共同构成一个新的WST-FP,如图4(h)所示,这是WST-FP的示意图
为种子流单元,标记为已访问。进入图4(f)中,并返回到类似于图4(b)中的流程。迭代继续,直到集合WST-FP中的每个流单元被标记为访问。最终,FP中的流单元共同构成一个新的WST-FP,如图4(h)所示,这是WST-FP的示意图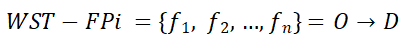 ,n表示 WST-FP 中的流单元数量,O 和 D 分别表示源区域组和目标区域组的时空属性。 然后,对于任何流单元
,n表示 WST-FP 中的流单元数量,O 和 D 分别表示源区域组和目标区域组的时空属性。 然后,对于任何流单元
 ,至少有一个流单元满足时空邻近性和阈值条件
,至少有一个流单元满足时空邻近性和阈值条件 。
。 的起始区域集可以表示为
的起始区域集可以表示为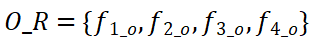 ,目标区域集可以表示为
,目标区域集可以表示为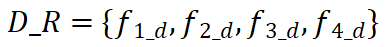
 。然后,共同构成
。然后,共同构成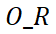 和
和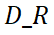
 共同构成WST-FPi基本空间特征量。
共同构成WST-FPi基本空间特征量。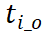
 ,每个 流量单元的目标区域对应一个到达时刻
,每个 流量单元的目标区域对应一个到达时刻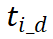
 。WST-FPi的起始区域的时间段可以表示为
。WST-FPi的起始区域的时间段可以表示为
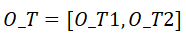 ,这里的
,这里的
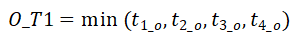 表示起始区域所有起始时刻中存在的最早起始时刻,表示最晚起
表示起始区域所有起始时刻中存在的最早起始时刻,表示最晚起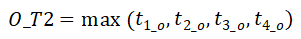 始时刻。同时,目的区域的时间段可以表示为
始时刻。同时,目的区域的时间段可以表示为
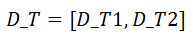 ,其中
,其中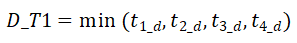
 表示目标区域所有到达时刻中最早到达的时刻,
表示目标区域所有到达时刻中最早到达的时刻,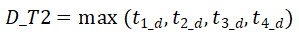 表示最晚到达的时刻。WST-FPi 的起始区域的持续时间为
表示最晚到达的时刻。WST-FPi 的起始区域的持续时间为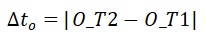 ,其目标区域的持续时间为
,其目标区域的持续时间为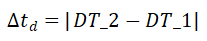 。 整个WST-FPi的持续时间为
。 整个WST-FPi的持续时间为
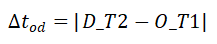 。
。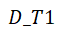
 ,and
,and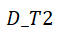 and
and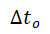
 ,
,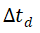
 ,
,  and
and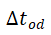 共同构成了WST-FPi的基本时间特征量(图5)。
共同构成了WST-FPi的基本时间特征量(图5)。

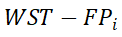 中相互作用体积之和与相同开始时间段或到达时间段的所有流单元的相互作用体积之和之比,用于反映整个流数据中目标流模式
中相互作用体积之和与相同开始时间段或到达时间段的所有流单元的相互作用体积之和之比,用于反映整个流数据中目标流模式
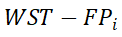 的重要性程度。在指定的时间段内
的重要性程度。在指定的时间段内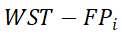
 的覆盖率公式可以表示为:
的覆盖率公式可以表示为: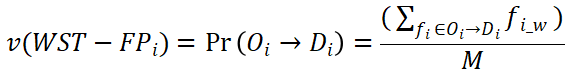
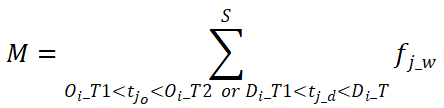
 是在时段
是在时段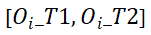 内从源区域
内从源区域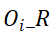 到
到
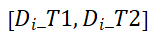 时段内的目标区域
时段内的目标区域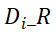 的概率。该流单元集合的开始时间在时段
的概率。该流单元集合的开始时间在时段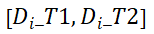 或时段
或时段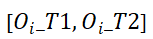 内。
内。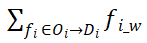 表示
表示
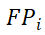 中的总交互流强度和.
中的总交互流强度和.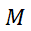 表示在时段
表示在时段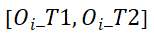 或时段
或时段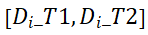 内的总交互流强度和.
内的总交互流强度和.
 的源区域集合都是
的源区域集合都是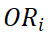
 ,从
,从
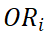 流出的总流用
流出的总流用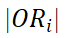 表示。目的区域的集合是
表示。目的区域的集合是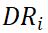
 ,到达目的区域的总流量用
,到达目的区域的总流量用 表示。对于任意一个
表示。对于任意一个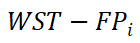
 , s值用来表示这个流模式的交互紧密程度。此外,利用s值反映流型中起点和终点区域之间的相关性强弱。计算公式为:
, s值用来表示这个流模式的交互紧密程度。此外,利用s值反映流型中起点和终点区域之间的相关性强弱。计算公式为: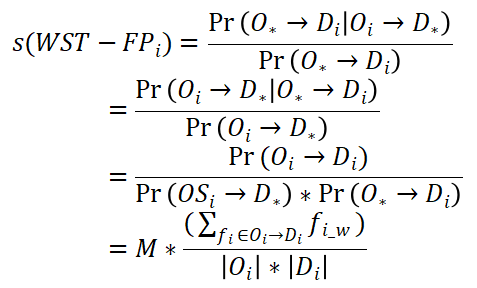

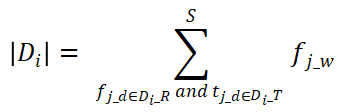

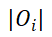 表示起源区域为
表示起源区域为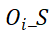
 、起始时间为
、起始时间为
 时段的流单元相互作用总量。
时段的流单元相互作用总量。
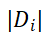 表示目的区域为
表示目的区域为
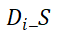 在时间段
在时间段
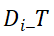 内到达时间的流单元的相互作用总量。
内到达时间的流单元的相互作用总量。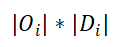
 表示从源区域到目的区域的总流量与总流量的乘积。
表示从源区域到目的区域的总流量与总流量的乘积。
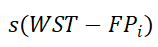 值越大,该流型的始发区与目的区之间的相关性越强。
值越大,该流型的始发区与目的区之间的相关性越强。 
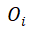 和目的
和目的
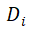 之间的相关性反映模式的强度。这两个指标从局部角度评价了WST-FP的强度,具有一定的局限性。本文采用覆盖率和准确率的综合值来综合反映模式的强度。具体公式为:
之间的相关性反映模式的强度。这两个指标从局部角度评价了WST-FP的强度,具有一定的局限性。本文采用覆盖率和准确率的综合值来综合反映模式的强度。具体公式为: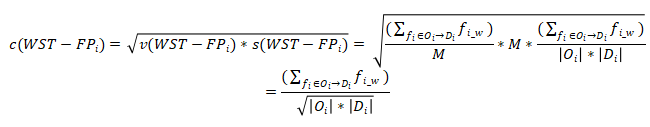


















 规划问道
规划问道







