南京市轨道交通车站客流特征析因及应用

城市轨道交通车站因区位、周边用地、线网构成特点等因素的不同，呈现不同的客流特征。对不同特征的车站进行分类，将有利于更合理、更精细化的轨道交通车站及周边配套设计。最直接、最具说服力的分类依据，是现状运营产生的轨道交通车站客流时空分布数据。然而未来的运营数据无可获知，若能建立基于现状运营数据的客流特征因子与其他指标(主要为居住人口、就业岗位及用地)间的回归关系，则能通过预期的规划指标预计车站未来的客流特征因子，进而对其进行分类。

文献[1]提出了“节点-场所”模型理论——轨道交通车站同时作为交通网络中的节点及城市空间中的场所，这两类特征的相对关系是车站类型划分的重要依据。文献[2]对国内外都市区轨道交通车站分类标准进行了总结分析，考虑因素主要为城市空间结构、轨道交通功能及其换乘特性、用地类型与开发强度等。文献[3]基于车站客流数据分别单独考虑时间特征、客流规模进行分类再组合。文献[4-5]从车站客流时间形态中提取部分指标，对车站类型进行划分。文献[6]利用车站所有分时段客流数据进行主成分分析，发现部分主成分可解释性较弱。文献[7]根据车站影响范围内用地类型的分布特征确定郊区车站分类。

基于现状城市轨道交通运营数据，本文提出一套可应用于规划或新建车站的分类分析方法。以南京市为例，利用2019年5—7月工作日平均的轨道交通车站分时段进出站数据(不含轨道交通系统内换乘客流)及手机信令数据，获取车站的接驳空间分布数据并开展研究。

城市轨道交通车站分类分析方法主要包括以下四部分。

1）析因分析。对各车站现状分小时上、下客数据以及高峰小时进站平均接驳距离(通过手机信令分析获得)通过因子分析降维，获取内在相互独立的影响因子。

2）聚类分析。以各车站各提取因子为输入，进行K均值聚类，获得现状分类结果及各类中心因子值(即分类标准)。

3）回归分析。采用多尺度加权回归方法，找到解释指标与因子值间的关系。解释指标主要为用地、居住人口、就业岗位、轨道交通车站节点属性(即车站可达性、连接线路条数等指标)。

4）规划应用。使用克里金插值法确定规划轨道交通车站因子与解释指标关系系数，计算解释指标得到规划车站因子值，可反映规划车站相对特征，亦可用于规划车站分类。

城市轨道交通车站客流特征解释维度广、指标多，若直接用于分类，一方面受输入指标的相互关联性影响，另一方面不同重要程度指标的权重也应有所不同，故分类结果的合理性直接取决于指标的选择，存在一定随意性。通过输入指标的因子分析，获取相互独立的若干因子再用于分类，可一定程度解决该问题。

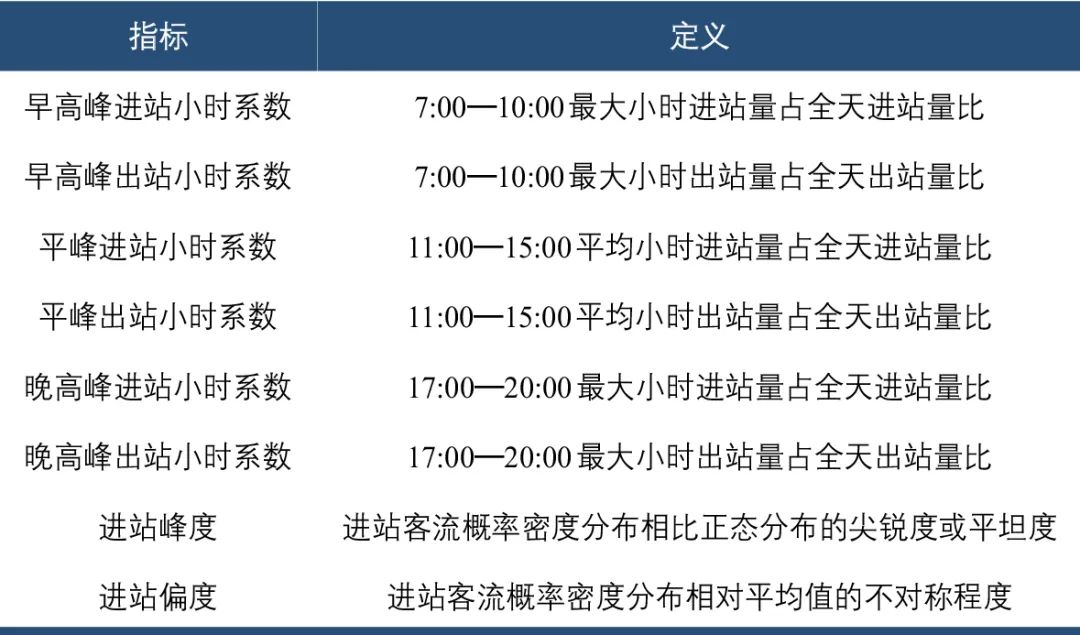
不同类型车站易呈现区分度较高的进出站全天时间形态差异，如进站双峰、左单峰、右单峰等。如何充分挖掘该时间序列，提取有代表性的指标，是因子分析的关键。常用的指标包括早高峰、平峰、晚高峰进出站小时系数^[3-4]。这些指标对构建大致的时间形态框架起到锚固作用，但容易丢失局部形态走向。

时间序列的结构特征是对时间序列全局构造或内在变化机制的描述，可表示全局特点^[8]。文献[5]增加进出站峰度、偏度及极大值个数，直接用于聚类取得了较好的车站时间形态区分效果，但指标可解释性不佳(预测未来每个车站的高峰系数等形态指标不具现实意义)。因此，宜通过因子分析提取具有实际意义的因子。输入因子分析的指标并非越多越好，必须反复测试，筛选有充分代表性的特征指标。

峰度、偏度基于概率统计分布得出，可补充挖掘形态信息。峰度(kurtosis)反映与正态分布相比某一分布的相对尖锐度或平坦度，其中正峰值表示相对尖锐的分布，负峰值表示相对平坦的分布。偏度(skewness)表明分布相对于平均值的不对称程度。不同软件的峰度、偏度计算公式有差异，本文使用EXCEL、SPSS的计算方法，公式如下^[9]

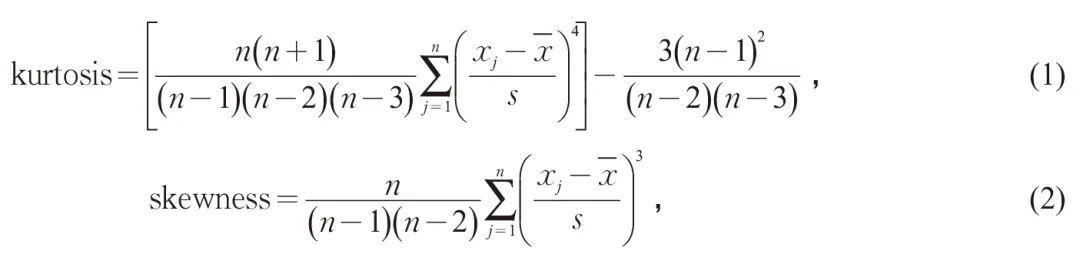
式中：n为样本数量；x_j为样本观测值j=1,2,⋯,n；为样本平均值；s为样本的标准偏差。时间序列自身分布形态与概率(频率)分布形态有较大差异，且与直观感受不同。概率统计分布是忽略时间顺序，按照数值量集计来统计频率的高低。某站(就业单一主导型)时间序列自身形态与概率分布差异见图1。

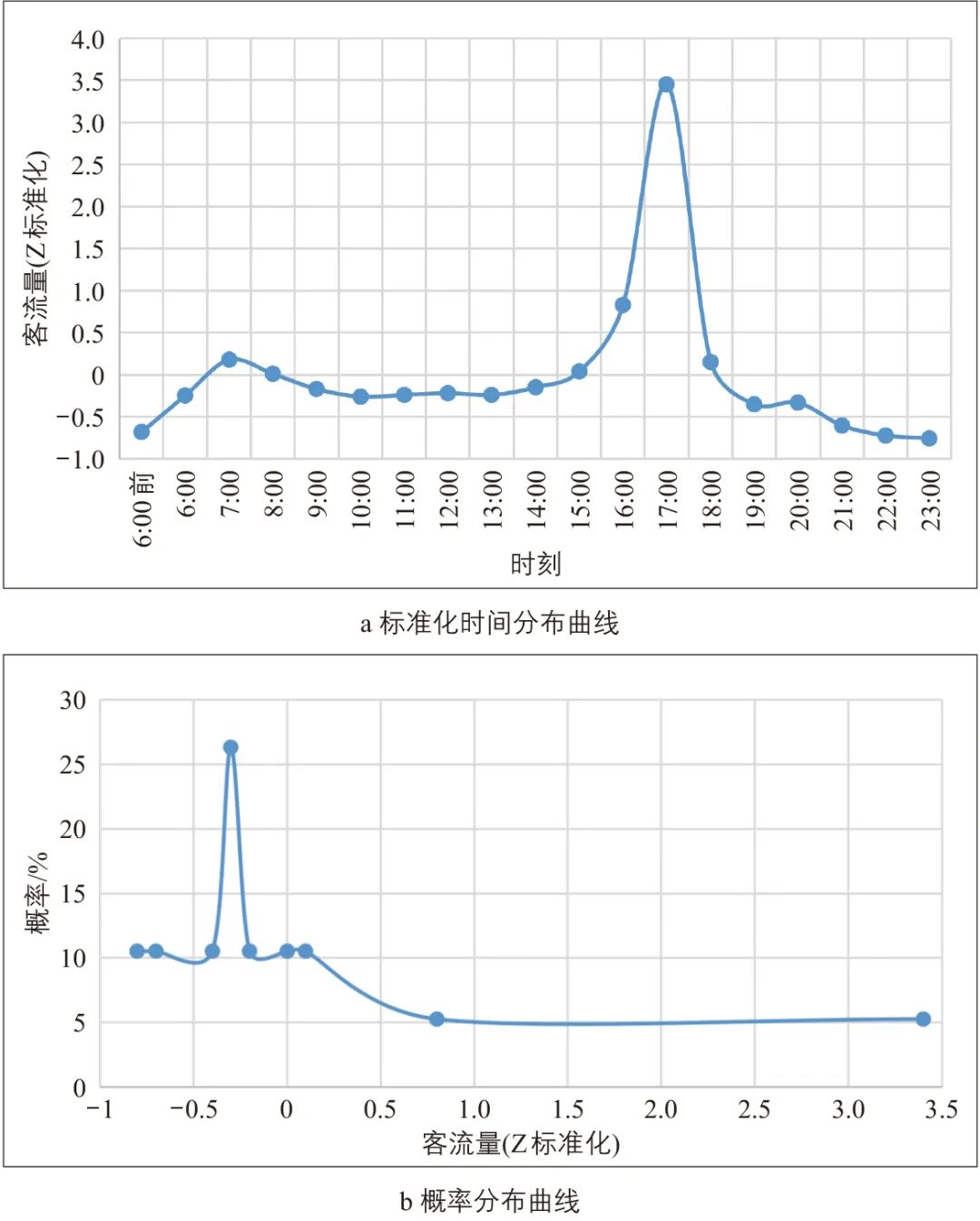
图1 时间序列自身形态与概率分布差异

从峰度看，枢纽、旅游类车站因客流较为分散，按小时统计的客流频率相差不大，即概率分布形态波峰较平缓；纯居住或就业类车站则较为陡峭。从偏度看，最大频率客流往往为平峰时期客流，对于枢纽、旅游类车站，最大频率客流相对较大，概率分布曲线尾部形态位于左侧，偏度较小；对于居住或就业单一主导的车站，最大频率客流相对较小，概率分布曲线尾部则位于右侧，偏度较大。为验证这一分析，通过人工判定部分车站类型并分别计算平均进出站峰度、偏度(见表1)。

表1 不同类型车站峰度、偏度特征验证分析

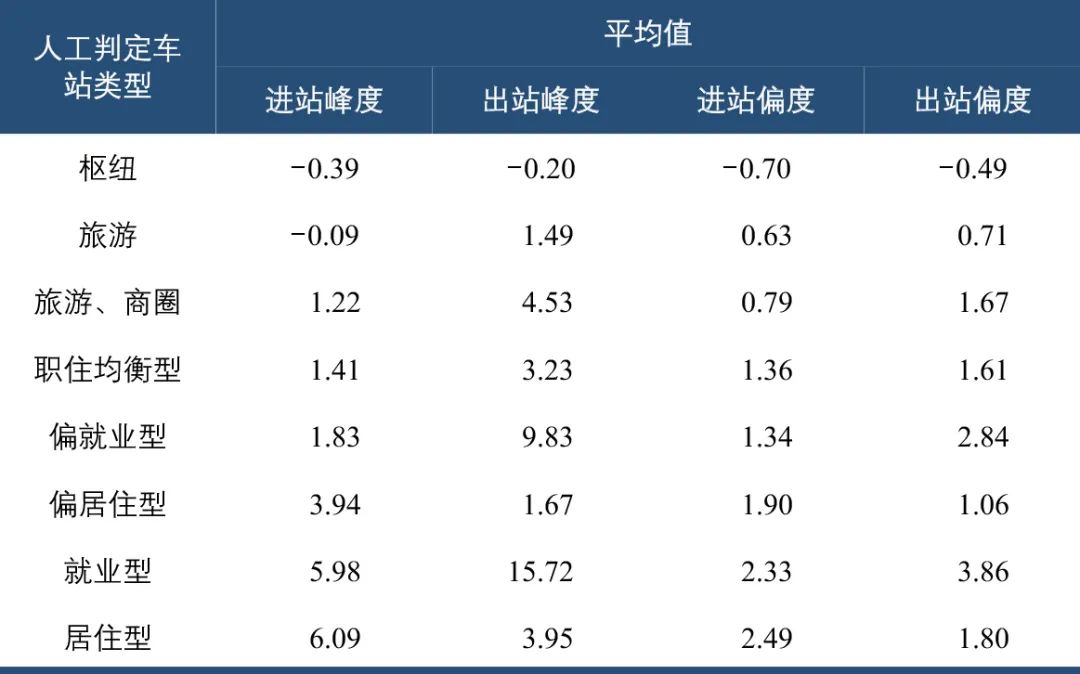
由表1可知，进站峰度与偏度符合以上分析，车站弹性越高(时间分布越分散)，峰度、偏度取值越低，对于出站则不完全符合。一方面，对于商业休闲车站，进站相对分散、出站相对集中(出站即进入该商圈，多为餐饮、购物集中时段；进站即离开，回程相对分散)；另一方面，居民出行回程晚高峰不如启程早高峰集中，同时由于通勤距离差异，晚间出站时间分散程度进一步放大，如居住主导车站，出站分布相对分散，与商业休闲类车站的区分度不大。因此仅选取进站峰度、进站偏度补充全局形态特征。时间形态特征选取指标如表2所示。

表2 时间形态特征指标

车站客流规模指标采用全天客流以对应全天形态，因全天进站、出站大致相当，故选用全天进站客流量。空间分布方面，早高峰通勤时段接驳范围能较好反映该车站的影响区域，同时因私有交通工具夜间通常停放于早高峰出发端，进站接驳较之出站接驳(出站步行接驳比例明显更大)更能体现真实影响范围。故依据南京市电信公司手机信令数据分析提取工作日7:00—9:00轨道交通车站平均进站接驳距离作为空间特征指标。

车站进站客流规模与平均接驳距离分布如图2所示。全天客流主要集中在中心城区，新街口站、南京南站工作日进站客流量达10万人次·d^-1(不含站内换乘客流，下同)，柳洲东路站、迈皋桥站、马群站、油坊桥站以早高峰通勤客流为主，进站客流量达3万~5万人次·d^-1。从早高峰平均进站接驳距离看，主城明显小于外围地区，核心区域小于500 m；首末站或线路转向处车站接驳距离较大，如马群站超过2.5 km；偏远车站客流较小、接驳范围更广，部分超过6 km。

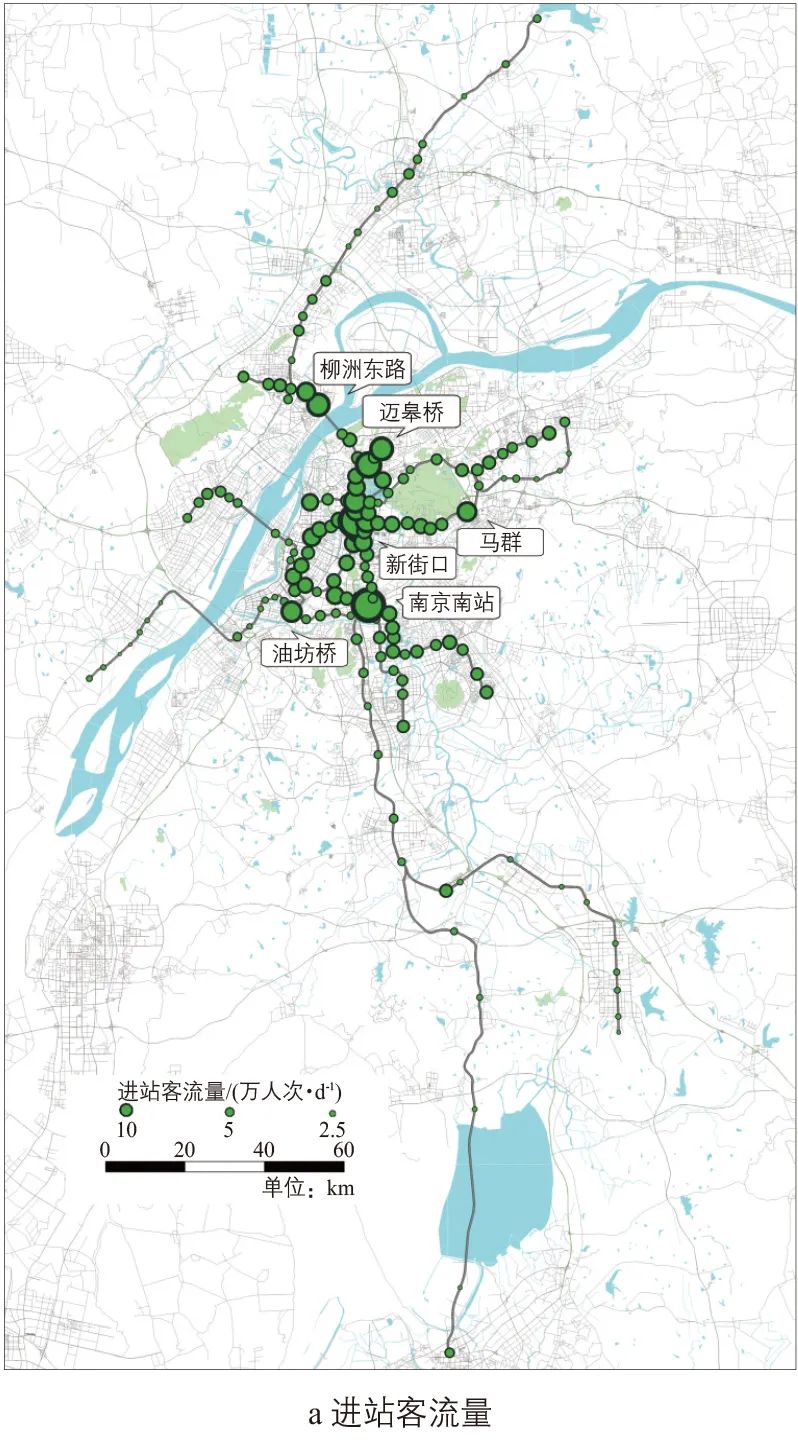
图2 现状工作日进站客流量与接驳距离分布

因子分析是将具有错综复杂关系的变量综合为数量较少的几个因子，以再现原始变量与因子之间的相互关系，探讨多个能够直接测量并且具有一定相关性的实测指标，是如何受少数几个内在因子支配的^[10]。

综合时间形态特征、客流规模及空间特征指标，使用SPSS因子分析工具进行降维，并通过因子旋转得到具有实际意义的因子。

本次因子分析采用Bartkett球形度检验法，得到变量间具有较强的相关性。KMO统计量高于0.7，说明信息间的重叠程度较高，适合因子分析模型。表3累计百分比反映前3个因子合计承载了超过80%的信息(累计方差)。

表3 提取因子解释的总方差

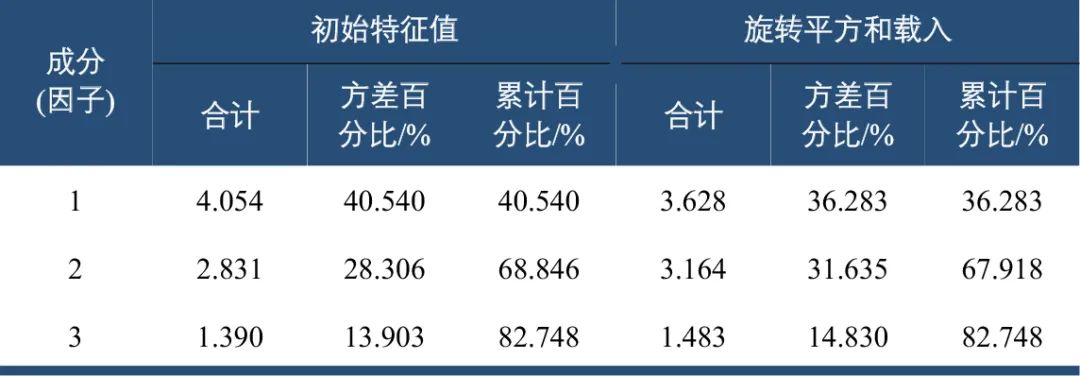
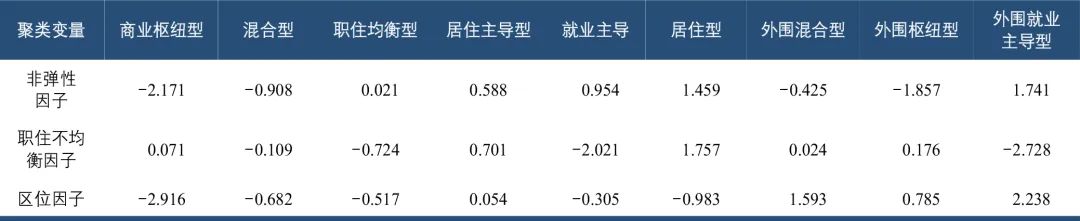
表4旋转成分矩阵表示每一个原始变量用因子表达时各因子的系数。因子1与平峰进出站小时系数强烈负相关，与进站峰度、偏度强烈正相关，与早高峰进站、晚高峰出站小时系数中等正相关；可知因子1表征非弹性、通勤出行比例的大小，命名为“非弹性因子”。因子2与晚高峰进站、早高峰出站小时系数强烈负相关，与晚高峰出站、早高峰进站小时系数强烈正相关；可知因子2表征居住人口与就业岗位的比例关系，命名为“职住不均衡因子”。因子3与工作日全天进站量强烈负相关，与进站来源平均接驳距离强烈正相关，位于主城的车站往往客流较大、接驳范围较小，外围车站反之，故命名因子3为“区位因子”。利用SPSS得出成分得分系数矩阵表(即每一个因子用原始变量表示时各原始变量的系数表)，进而得到各因子值(原始变量应先进行Z标准化)。现状各车站的因子属性特征如下。

表4 旋转成分矩阵

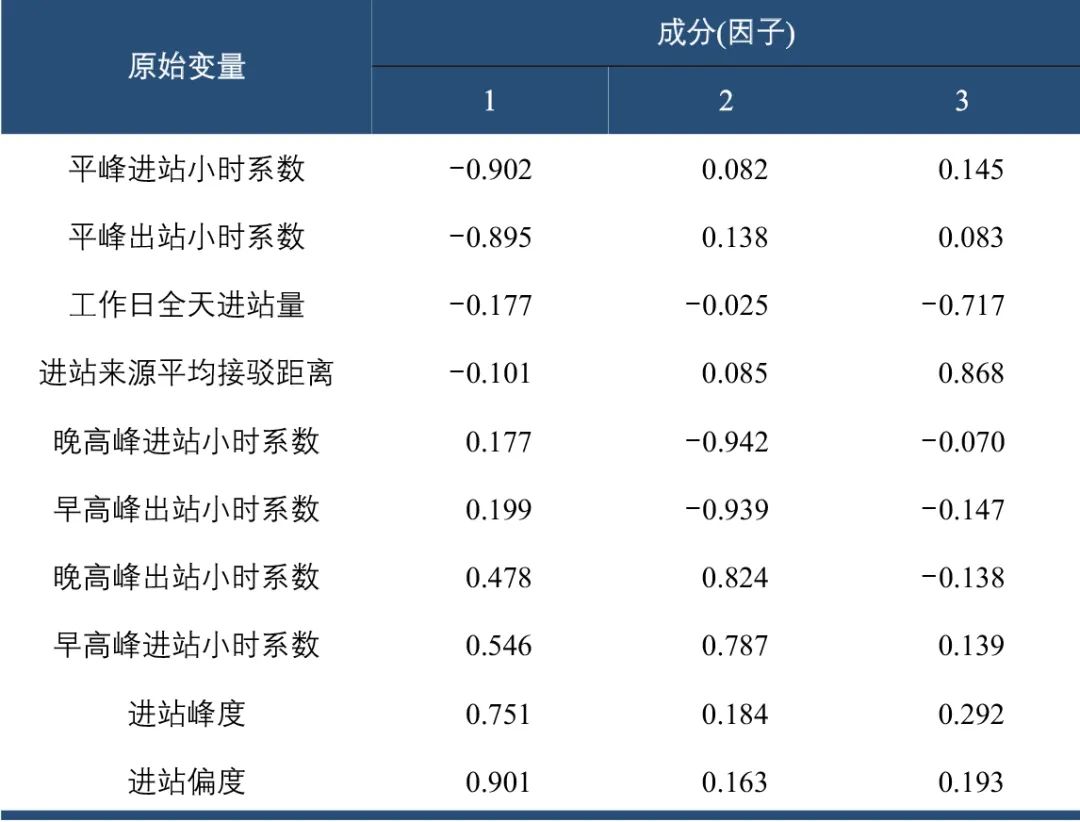
注：提取方法为主成分法；旋转法为具有Kaiser标准化的正交旋转法。

1）非弹性因子：居住集中地(如天润城站)非弹性因子很高(即通勤出行比例很高)；城市中心很低(即弹性出行比例很高)。通勤出行比例较高的车站多围绕主城分布(见图3a)。

2）职住不均衡因子：纯居住、就业类车站职住不均衡因子绝对值较高且分别为正值、负值，因为该因子与居住呈正相关、与就业呈负相关，如居住集中的天润城站与就业集中的苏宁总部徐庄站；并非所有通勤比例较高的车站职住不平衡因子绝对值均较大，如铁心桥站非弹性因子(即通勤比例)较高，但其职住不平衡因子绝对值较低，说明其周边居住人口、就业岗位较为均衡，但休闲、娱乐等产生弹性出行的设施较少(见图3b)。

3）区位因子：整体呈现中心城区小、外围大的特征；部分外围车站地处相对独立的城镇，其区位因子也不至于过大，如溧水的中山湖站、六合的龙池站(见图3c)。

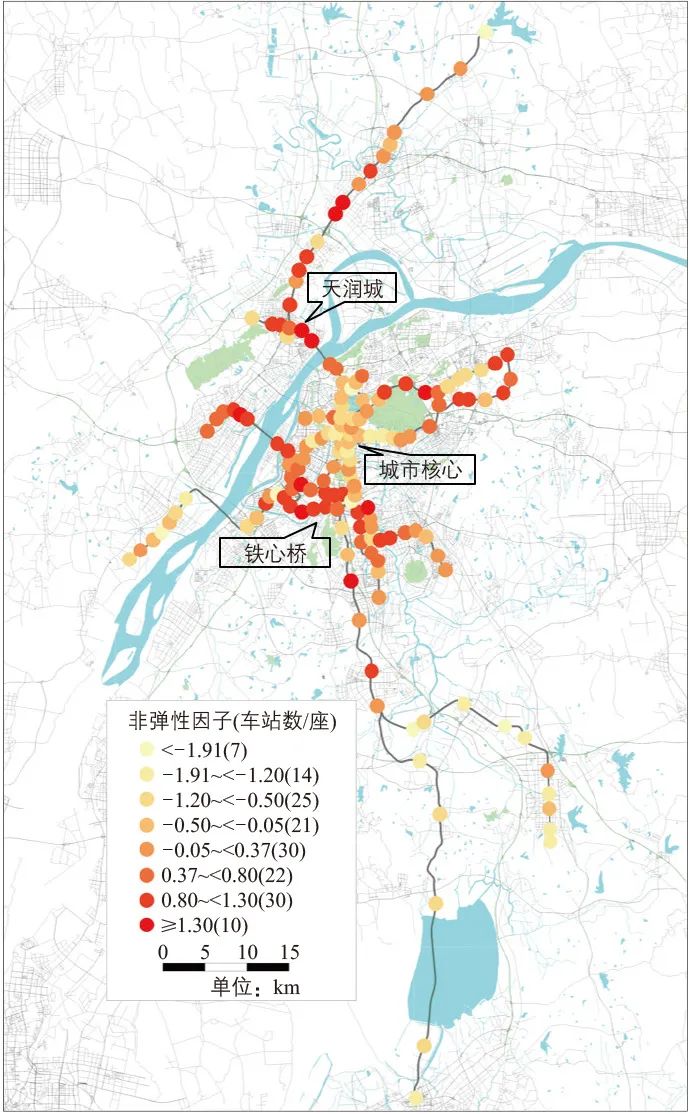
a 非弹性因子

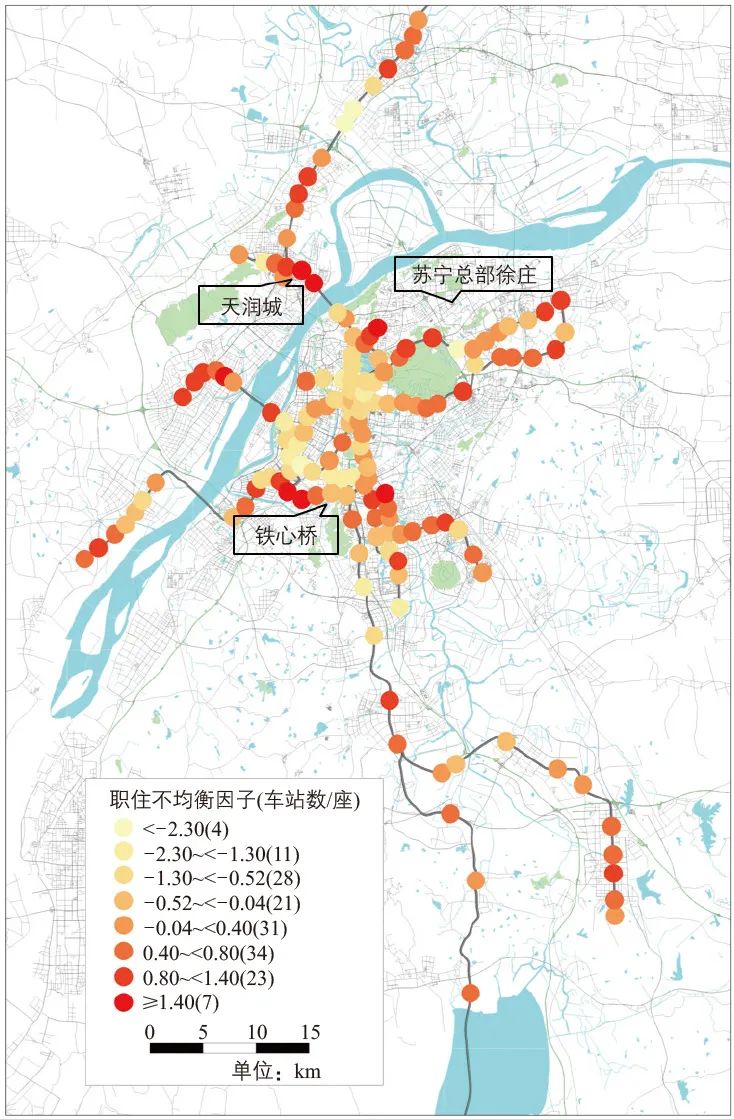
b 职住不均衡因子

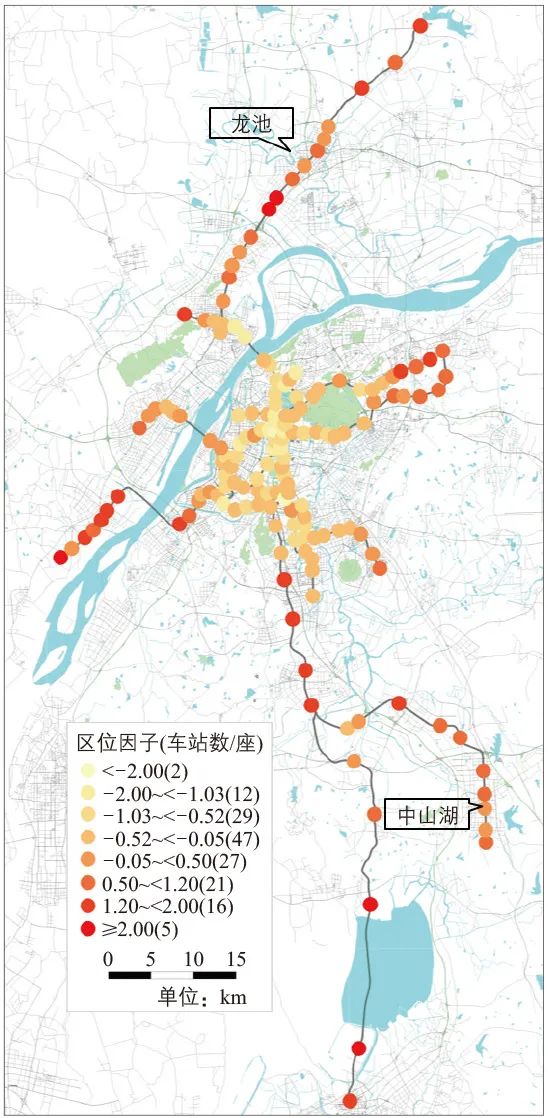
c 区位因子

图3 现状各车站的因子属性特征

注：括号中数值为车站数/座。

在获得各车站3个因子的基础上，使用聚类方法得到车站分类。常用的聚类方法为层次聚类法与K均值聚类法。层次聚类法为按照空间距离逐渐由单独个体合并为一类的方法(或反过程，本质相同)，一次得到所有分类数的分类集合。因其按照空间距离顺序逐个合并，有时对于指定的分类数，存在分类极不均匀的情况。而对于实际研究对象，可能需对不同区域有不同的分类间隔阈值，如核心区分类间隔阈值较低，外围分类间隔阈值较高。故采用K均值聚类法——通过指定分类数目、指定或自动设置初始类中心，计算确定初始分类并计算新中心、新分类……如此往复迭代。因其设立初始的分类中心，相对于层次聚类可获得更符合实际需求(分类更均匀)的分类结果。

K均值聚类需要指定分类数量。分类的数量与需求有关，因为每个样本之间均存在差异，极端情况每个样本都可成为一类，但分类太细已失去原本意义，因此需要把握分类精度与合并归类带来的便捷性应用的平衡，确定分类合理范围。

对于本研究需要反映的车站时空客流特征，首先根据客流时间形态进行判断，按进站时间形态(出站形态类似)至少有左单峰、右单峰、双峰且平峰较低、双峰且平峰较高、全天较平均5种；若同时考虑区位与客流规模，则外围客流相对低区域也至少有双峰、右单峰(外围客流低区域很少出现全部集中于早高峰的左单峰)、全天较平均3种。因此，分类至少为8类。分别测试8~10类的分类情况，并以9类为基准说明异同(见表5)。综合考虑类型区分度与应用便捷性，车站的聚类结果以9类划分。经方差分析，各类别间3个因子均有显著差异，且具有统计学意义。

表5 不同分类的差异分析

南京159个轨道交通车站(换乘站不重复计)的具体类别为：

1）商业枢纽型，城市弹性出行比例最高、平峰客流较大；

2）混合型，弹性出行平峰客流不及商业枢纽型，用地较为混合；

3）职住均衡型，进站客流时间形态呈现双峰，但平峰客流较低，居住、就业人口较为均衡；

4）居住主导型，进站客流时间形态偏向左单峰，以居住为主，有少部分就业；

5）就业主导型，进站客流时间形态为右单峰或偏向右单峰，以就业为主，可能有少部分居住；

6）居住型，进站客流时间形态为左单峰，基本为纯居住；

7）外围混合型，指城市外围居住、就业较为混合的车站；

8）外围枢纽型，指城市外围客流来源较为分散，峰值不明显的车站；

9）外围就业主导型，指城市外围以就业为主的车站。

该分类中的“外围”指接驳覆盖范围较大、客运量较小的车站，一般位于城市外围，但不排除部分外围车站由于周边设施布局影响使接驳范围较小而并未划入。

车站所属类别及客流时间形态如图4所示。各聚类中心因子值见表6，由此可基于与各类中心欧式距离的大小判定类别的归属。

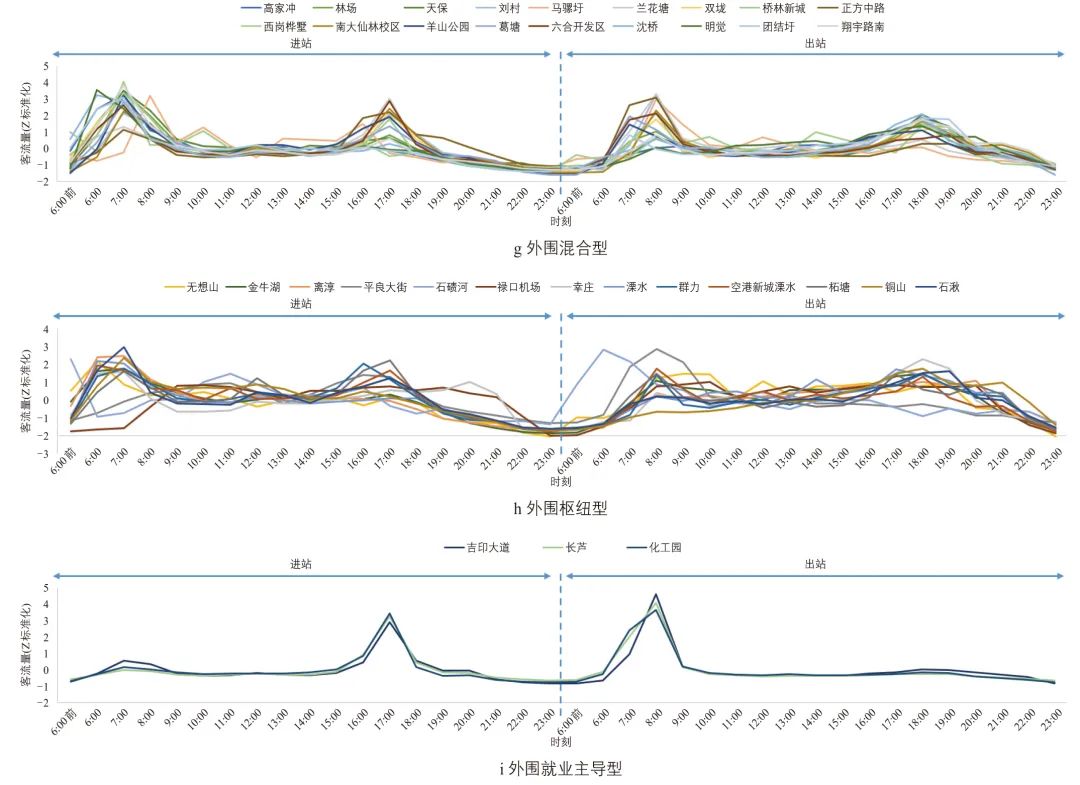
图4 各类车站客流时间形态

表6 聚类中心因子值

为了获得规划轨道交通车站的因子值，应建立其他指标与因子间的回归关系。

传统的最小二乘法(Ordinary Least Squares, OLS)回归假设所有特征因素存在同质性。而对于轨道交通车站客流，不同车站的周边交通环境不同(如城市中心停车不便)，不同区域乘客的交通倾向性不同(如部分区域居民家庭较富裕，家庭拥车比例较高)以及各种其他复杂的地域相关性因素，使得统一的OLS回归模型难以获得满意的解释效果。

经典地理加权回归(Geographically Weighted Regression, GWR)考虑空间自相关，将数据的空间位置嵌入回归参数，基于局域回归分析和变化参数使用局部加权最小二乘估计方法进行逐点参数估计，其优势在于可以处理空间异质性^[11-12]。

多尺度地理加权回归(Multiscale Geographically Weighted Regression, MGWR)是GWR的进一步拓展，其计算公式为

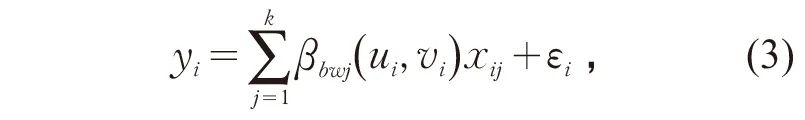
式中：y_i为第i个样本点因变量值；(u_i,v_i)为第i个样本点的地理空间坐标；β_bwj(u_i,v_i)为第i个样本点的第j个变量使用bwj带宽的回归系数；x_ij为第i个样本点的第j个自变量值；k为自变量的总个数；ε_i为随机误差项。相比于GWR，MGWR的每个变量都可以有不同的带宽(尺度或者说影响范围)，每个回归系数都基于局部回归得到。不同变量(影响因素)往往存在不同的异质性和尺度，即在某个范围内作用大小相似，超过该范围则作用差异明显^[13-14]。本文中各因子对区位较为敏感，不同区域家庭富裕程度、出行习惯不同。因此，对各因子使用MGWR模型进行解释，运算软件为美国亚利桑那州立大学空间分析研究中心开发的MGWR2.2软件，使用常用的二次核函数和AICc准则，模型形式均采用线性模型，各变量数值均标准化^[15]。

非弹性因子与区位、用地布局、居住人口和就业岗位规模以及轨道交通车站的节点属性有关。

1）城市中心系数。

城市中心系数反映区位影响，借鉴重力模型形式构建非线性公式，城市中心系数=，式中：G，b，r为需标定参数；i为当前城市中心数量；k_i为城市中心等级系数(依据城市现状人口分布定量、定性确定，未来结合规划定位与发展确定)；T_i为车站至第i个中心的公共交通时耗/h。

现状城市中心根据人群活动集聚情况确定，基于手机信令人群活动热力值定量判断分级取值(考虑到实用性，根据规划区位层级略做调整——相近的区位层级取值一致)：新街口中心k取10，城南中心、河西中心k取3，东山副中心、仙林副中心、六合副中心k取1.5，溧水副中心、高淳副中心k取1。以车站500 m范围内人数(通过工作日15:00手机信令数据获取)表征车站的城市中心系数并作为因变量，计算各车站至各中心的公共交通时耗T_i，使用SPSS进行非线性拟合，得到估计值：G=580.06，b=1.786，r=0.067，其中拟合优度R²=0.893。

2）分圈层用地面积。

轨道交通车站周边土地利用价值较高，且不同圈层的影响有所不同。故以500 m为间隔分圈层统计每个车站影响范围内的用地类型。实际上在不同区位用地作用亦明显不同，应结合用地开发强度进行统计，但由于数据资料有限，同时考虑到MGWR对变量在不同区域拟合了不同系数，对开发强度及其他因素的考虑已一并体现在对应系数中，故在此仅直接统计用地面积。考虑不同用地对出行产生的影响，将用地类型划分为18类，分别为：居住、行政办公、商业、文化娱乐、医疗卫生、中小学、体育用地、市政公用设施、仓储用地、商住混合、商办混合、科研、大专院校、商务、交通枢纽、景区公园。

利用基于最短路径的扩展泰森多边形建立车站影响范围^[16]，即将仅计算直线距离的泰森多边形拓展至考虑拓扑路网距离。各车站影响范围见图5，主城区车站影响范围小，外围车站影响范围大，但还需根据轨道交通车站实际辐射能力进行裁剪。变量包括0~500 m，>500~1 000 m，>1 000~1 500 m三个圈层内每类用地的面积。

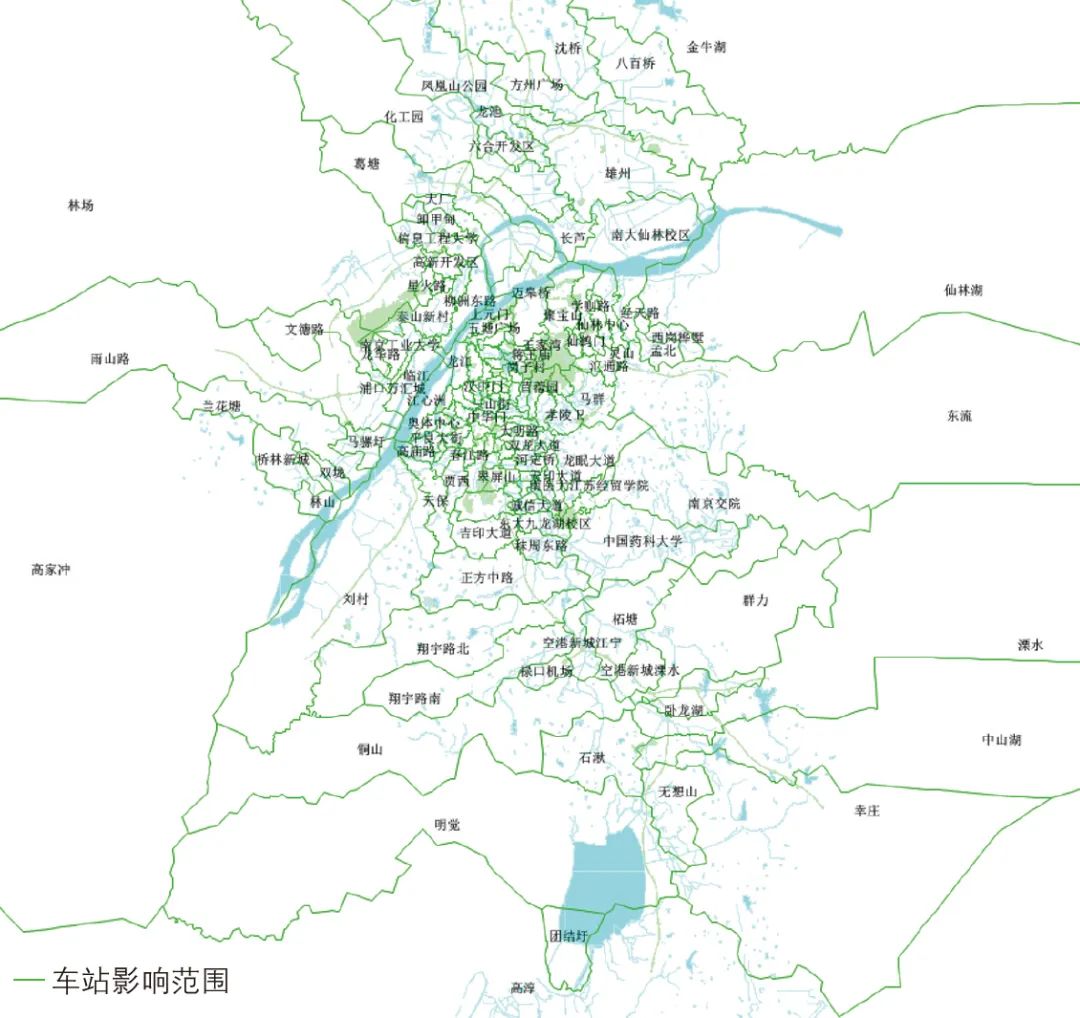
图5 轨道交通车站影响范围

3）其他变量。

其他变量还包括车站影响范围1 000 m内居住人口、就业岗位总量(通过手机信令数据识别)，以及轨道交通40 min可达车站数(从本车站出发40 min可达的车站数)。

MGWR调整拟合优度值0.728远高于统一的OLS模型值0.213。从各变量的系数值来看，以影响范围1 000 m内总居住人口系数为例(见图6)，呈现外围较大、中心较小的特点，说明外围居住人口对使用轨道交通通勤的人均贡献大于中心居住人口。

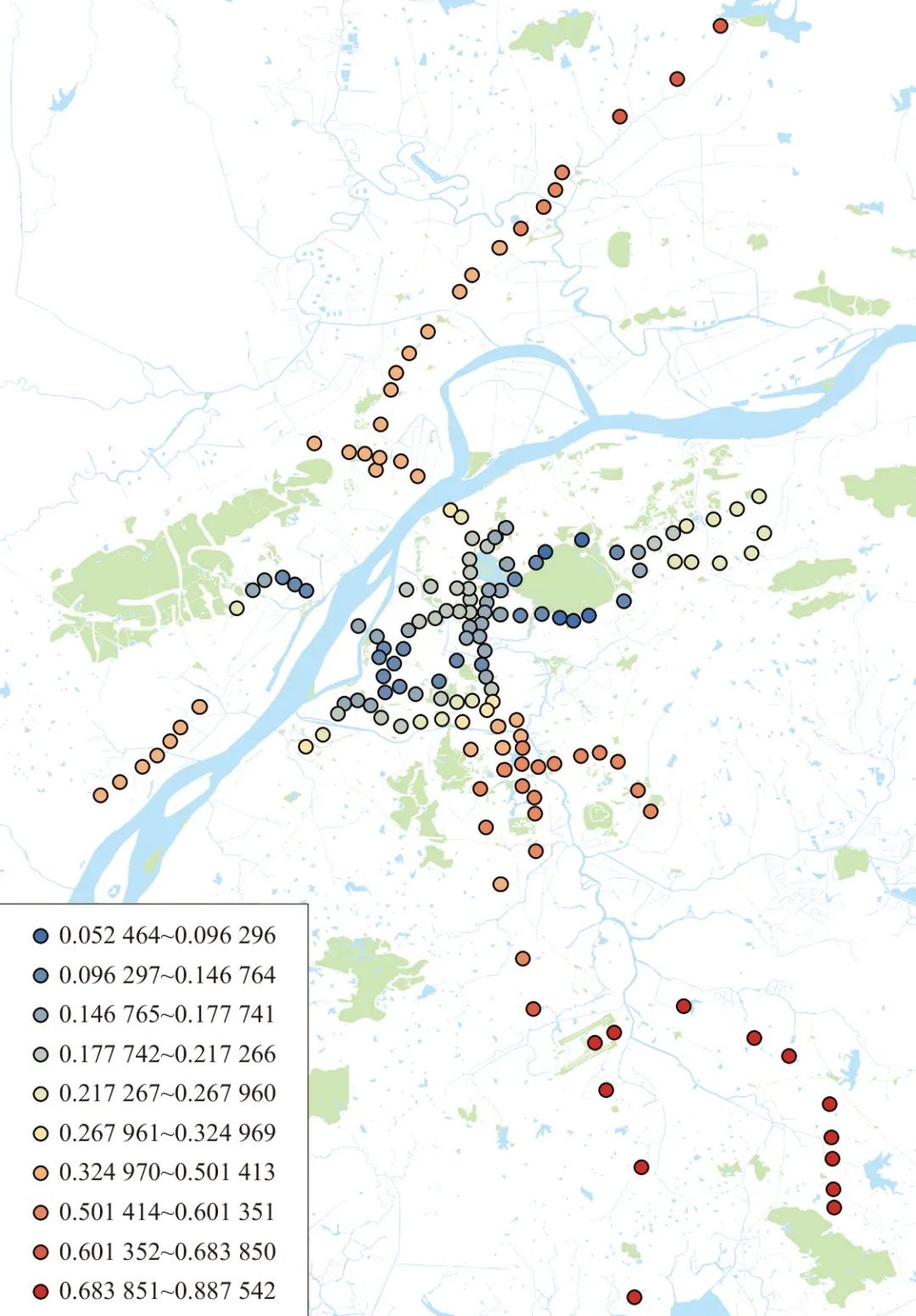
图6 在非弹性因子回归中影响范围1 000 m内总居住人口变量系数

职住不均衡因子主要与居住人口、就业岗位的相对关系以及轨道交通车站的节点属性有关。

1）居住人口与就业岗位相对关系。

分别在0~500 m，>500~1 000 m，…，>2 000~2 500 m五个圈层构建指数、线性、对数三种形式的居住人口与就业岗位相对关系，分别为：指数形式，线性形式，对数形式。其中pop与job分别为对应圈层的居住人口、就业岗位数，为避免部分车站没有外部圈层或外部圈层数值为0而产生错误，故加上0.000 1。

2）其他变量。

其他变量还包括影响范围内五个圈层的居住人口、就业岗位绝对数，轨道交通40 min可达车站数、车站通过轨道交通线路数。

MGWR调整拟合优度值0.732高于统一的OLS模型值0.661。从各变量的系数值来看，以轨道交通40 min可达车站数的系数为例(见图7)，主城南部为正、主城北部和外围为负，反映现状主城南部完善的轨道交通线网加剧了主城区的职住不平衡，而外围由于相对独立，线网的完善反而对职住平衡有促进作用。

图7 在职住不均衡因子回归中轨道交通40 min可达车站数变量系数

区位因子主要与车站影响范围及客流规模有关。因此，选取的变量包括：等效半径(车站影响范围按7 km半径进行裁剪，将统计得到的不规则图形面积换算为等量圆的面积，该等量圆的半径即为等效半径。以7 km为半径是因为手机信令数据显示车站7 km范围内包含了绝大多数轨道交通客流)、0~2 500 m五个圈层的居住人口与就业岗位数(以500 m为间隔)、轨道交通40 min可达车站数、通过车站的轨道交通线路条数。

MGWR调整拟合优度值0.826高于统一的OLS模型值0.724。从各变量的系数值来看，以车站影响范围按7 km裁剪的等效半径的变量系数为例(见图8)，南部高于北部，说明同样影响范围的外围车站，南部的客流更小，这也与现状宁溧、宁高线客流较小的现实相符。

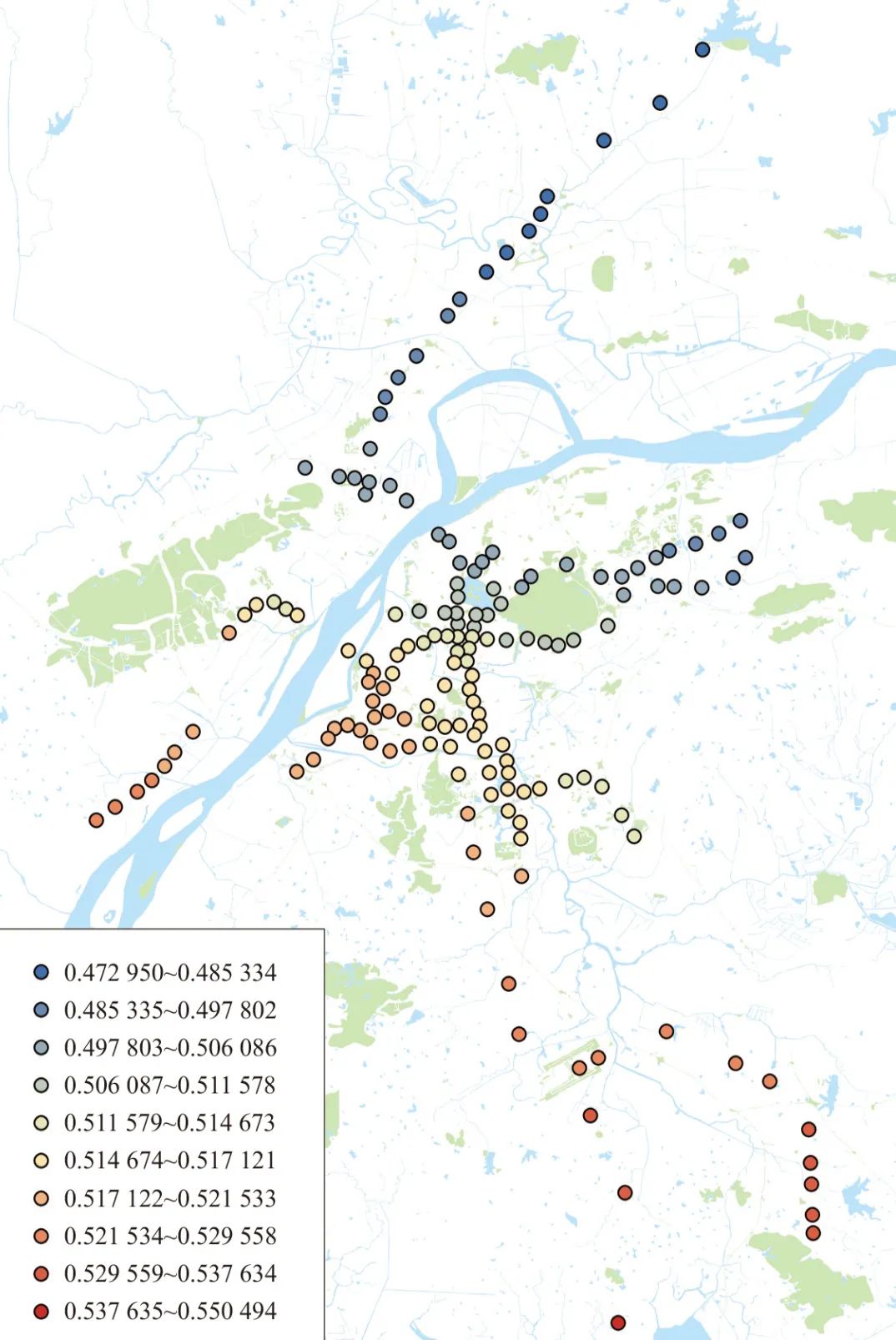
图8 在区位因子回归中等效半径变量系数

基于2019年修编的《南京市轨道交通线网规划》中2035年线网，以及该年度用地布局、居住人口和就业岗位预测等资料或数据，进行应用举例。

因使用MGWR方法回归得到的各变量系数呈地理位置相关的连续分布，规划车站需进行插值确定。采用克里金插值法，假定采样点之间的距离或方向可以反映表面变化的空间相关性。将数学函数与指定数量的点或指定半径内的所有点进行拟合以确定每个位置的输出值^[17]。其公式为

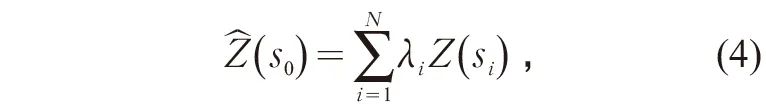
式中：为预测位置的插值结果(此处即为规划车站回归系数)；Z(s_i)为第i个位置处的测量值(此处即为现状车站回归变量系数)；λ_i为第i个位置处的测量值的未知权重；s₀为预测位置；N为测量数值。采用ArcGIS克里金插值工具箱，编写脚本并对所有变量系数进行批量插值。

获取规划车站变量值(Z标准化)及利用式(4)获取的回归系数后，代入式(3)得到各车站因子值，依据表6计算与各类别中心的距离并判定归属。分类结果如图9所示，规划线网建成情况下，主城依然为商业枢纽型、混合型车站集聚地；江北新区依据规划高定位，部分车站转变为商业枢纽型、混合型车站；外围相对独立的副城中心也将转变为混合型车站，如溧水站。

需要说明的是，规划年车站分类仅为规划车站因子值的部分应用，且可能存在规划不确定性大、现状分类或许不再适应等问题。然而，规划车站因子定量呈现了弹性出行与通勤出行比例、职住不均衡性、区位特征等，其相对关系可为相关分析提供参考。

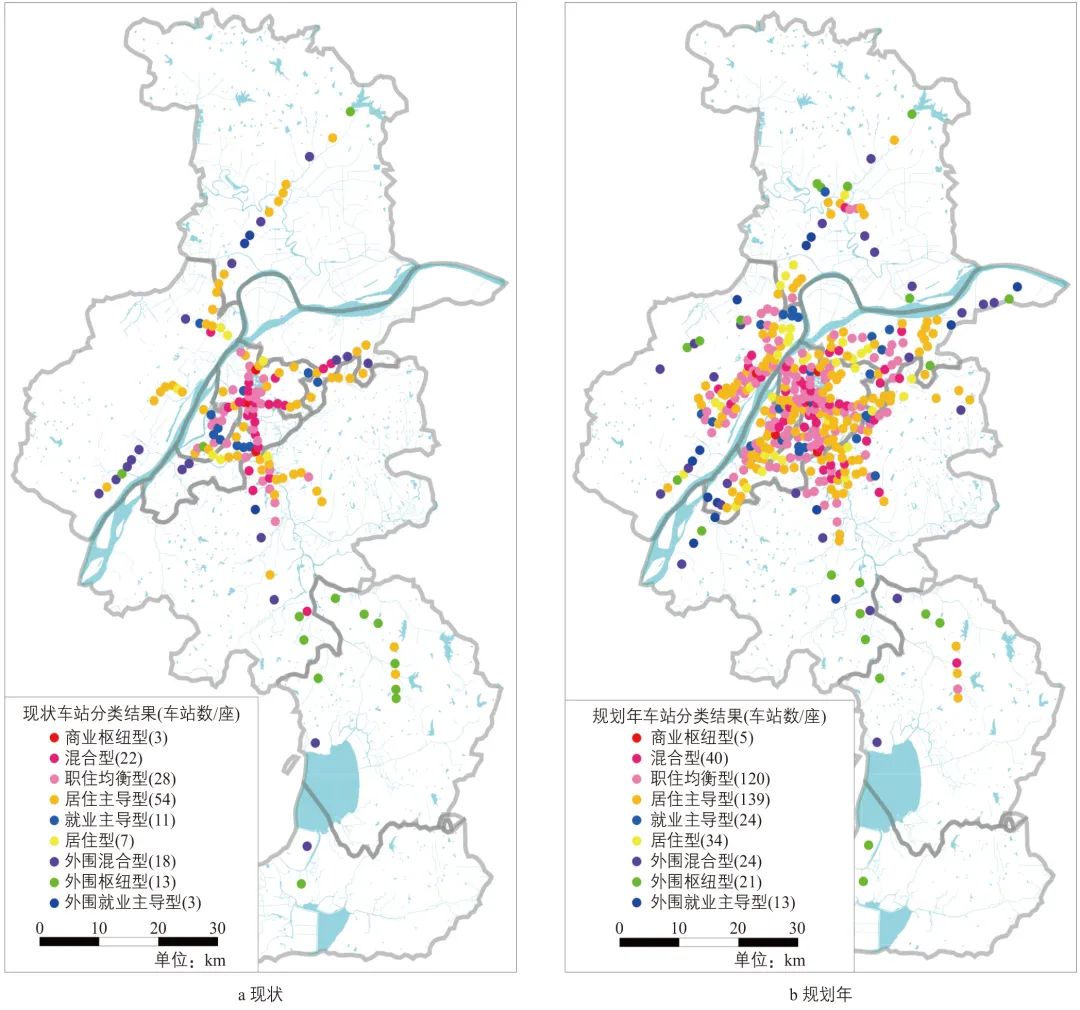
图9 现状与规划年车站分类结果对比

根据不同车站的时间形态特征规律，发现在高峰、平峰小时系数基础上补充进站偏度、峰度，可补充挖掘时间形态信息并获取有实际意义的因子，进而考虑客流规模及空间分布特征，通过因子分析提取了非弹性因子、职住不均衡因子、区位因子，使因子解释成为可能。

有关人的行为成因复杂，使用传统的最小二乘法，难以对因子进行较好的解释。MGWR考虑了空间异质性及变量尺度，即考虑地理位置的相关性并使变量影响范围可变，可获得更好的解释效果。

在数据资料允许的情况下，统计用地面积时考虑开发强度将进一步提高MGWR变量系数的可解读性。预测的规划人口、就业岗位分布直接影响规划年各因子结果。因此，预测居住人口、就业岗位分布宜在现状人口分布的基础上，考虑增量人口在增量用地上的分布以及新建轨道交通车站对居住人口、就业岗位的聚集作用^[18]。

周边城市功能的完善程度、步行系统的便捷程度、道路交通的拥堵程度都会较大概率地影响车站的客流量，未来对于区位因子的解释分析可考虑以上因素，建立如步行可达性的定量指标来进一步提高解释准确度。此外，由于规划的轨道交通线位及车站位置通常尚未稳定，故应强调定量与定性相结合的方法。

本文对于现状与未来MGWR模型各变量系数不变的假设，可能并不符合实际。但从事物发展规律看，规划不可能脱离现状产生颠覆性改变，因此该假设也具有一定现实性。变量系数未来的变化以及模型的适当简化有待进一步研究。

《城市交通》2021年第2期刊载文章

作者：戴骏晨，凌小静，

彭艳梅，韩竹斌